|
D - Lois de probabilités
1. Préambule
2. Quelques rappels sur les probabilités
3. Définition : 2 cas à considérer
4. Exemples
5. Loi Binomiale
6. Loi de Poisson
7. Calcul de probabilités dans le cas des lois de distribution continues
8. Loi Normale
9. Passage d'une loi binomiale à une loi normale
10. Some more training
11. Fluctuation d'échantillonage d'une proportion expérimentale (observée)
12. Travail avec R
Lois de probabilités
1. Préambule
Loi de probabilité : élément central de la statistique
Avant tout, il faut bien définir la VA d’étude
La détermination de la loi de probabilité suivie par une variable va servir :
- aux calculs de probabilité de réalisation d'évènements,
- à la déduction
- à l'inférence statistique
Déduction :
prédire, à partir d'une population connue ou supposée connue, les caractéristiques des échantillons qui en seront prélevés
Induction (inférence) :
prédire les caractéristiques d'une population inconnue à partir des statistiques déterminées dans un échantillon représentatif de cette population.
Extrapolation des observations réalisées dans un échantillon à l'ensemble de la population
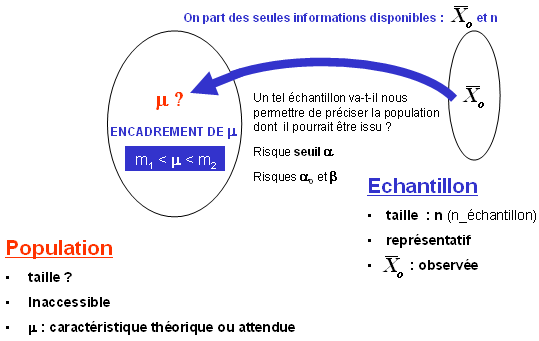
Notations

Intéressons-nous, par exemple, à l’information “moyenne”
On étudie les populations à partir d’échantillons (représentatifs)
Epreuve :
expérience
- qui peut être reproduite dans les mêmes conditions autant de fois que l'on veut,
- dont le résultat n'est pas prévisible
- et pour laquelle on peut définir l'ensemble des résultats possibles.
L'évènement :
est un sous ensemble des résultats possibles de l'épreuve.
2. Quelques rappels sur les probabilités
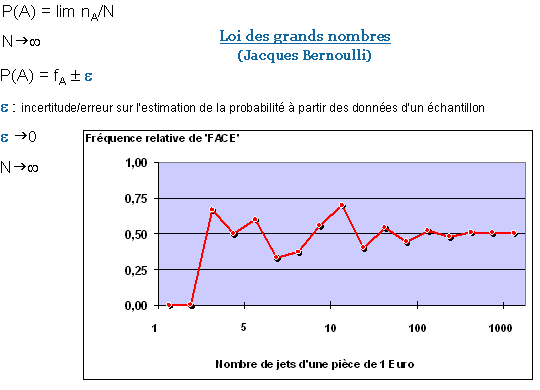
Probabilité
Définition 1
probabilité p(E) d'un évènement E : limite de sa fréquence relative.
répétition de l’épreuve un grand nombre de fois (n)
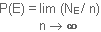
Définition 2
La probabilité p(E) d'un évènement E, lors de la réalisation d'une épreuve, est un nombre compris entre 0 et 1. (0 correspond à un évènement impossible et 1 à un évènement certain). La probabilité de E sera d'autant plus grande que E se produira fréquemment.
De façon schématique :

Définition 3

Origine :
le jeu de dés fut, il y a plusieurs centaines d'années, à l'origine de la théorie des probabilités
Une notion importante intervenant en statistiques dans :
- la définition des modèles probabilistes (lois de probabilités) ;
- la mesure du degré de confiance que l'on peut accorder aux modèles
Exercice "L'examen de TP"
On fait passer l'examen de TP de biochimie aux étudiants de master d'une grande université (250 inscrits). L'examen consiste en 2 manips, M1 et M2, notées chacune sur 10. Un étudiant "réussit" une manip s'il obtient au moins la note de 5/10 à cette manip. Un étudiant est reçu à l’examen de TP s’il a réussi les deux manips.
On constate que la probabilité de réussir la manip M1 est de 0,5. La probabilité de réussir la manip M2 est, quant à elle, de 0,6. Enfin, la probabilité qu'un étudiant réussisse la manip M2 alors qu’il a réussit la manip M1 est de 0,8.
Q1 : Réussir M1et M2 sont-ils deux évènements indépendants ?
Reponse : non car P(M2/M1) 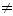 P(M2) P(M2)
Q2 : Quelle est la probabilité d’être reçu à l’examen de TP de biochimie ?
Réponse :

3. Définition : 2 cas à considérer
| Une définition très simple … |
Une loi de probabilité
est entièrement définie par l’ensemble des valeurs possibles prises par la variable aléatoire et les probabilités d’apparition de chacune de ces valeurs. |
... qui demande un peu de précision |

Espérance ou moyenne théorique d’une loi de distribution
Barycentre de la distribution
(valeur pas toujours prise par la variable!)
Moyenne (moment d'ordre 1) :
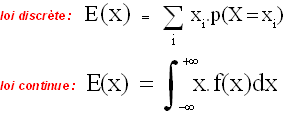
Variance :
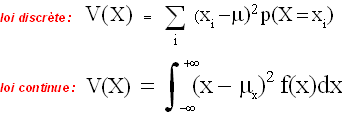
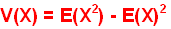
Exemple introductif
Considérons un caractère dû à un gène ayant deux allèles A et a. Si les parents sont tous deux hétérozygotes (ont le génotype Aa), les génotypes de leurs descendants sont l'un des 4 types suivants : AA Aa aA aa. Si ces évènements sont également probables, la probabilité de chacun d'eux est 1/4.
On obtient une première loi de probabilité :

Si de plus, le gène A est dominant, les individus de génotype AA, Aa et aA ont le même phénotype et la probabilité d'obtenir ce phénotype est 3/4.
On obtient finalement la loi de probabilité suivante :

Le modèle ainsi défini convient à l'étude de nombreux croisements (ex pois étudiés par Mendel, le caractère étudié pouvant être par exemple la couleur des fleurs)
Exercice "les pois de Mendel"
Soit le croisement de pois à fleurs jaunes (A, caractère dominant) et vertes (a). Calculer la probabilité qu’une plante à fleurs jaunes de la deuxième génération (c’est-à-dire obtenue par croisement de deux hétérozygotes) soit hétérozygote.
Solution
Soit J : « les fleurs sont jaunes » et H : « la plante est hétérozygote »
La probabilité recherchée est P(H / J) («fleur jaune» est le caractère établit)
En se servant de la loi de probabilité établie auparavant :

Commentaire
Les évènements (génotypes) ont été pris ici également probables.
Ce modèle ne convient pas aux primevères pour le caractère des feuilles plates (A) ou ondulées (a) : la fréquence expérimentale du nombre de feuilles plates est voisine de 4/5
(les plantes à feuilles ondulées sont moins viables que celles à feuille plates).
 Seule l’expérience permet de décider si les valeurs attribuées aux probabilités sont ou non satisfaisantes pour la description du phénomène étudié. Seule l’expérience permet de décider si les valeurs attribuées aux probabilités sont ou non satisfaisantes pour la description du phénomène étudié.
 Le modèle statistique doit tenir compte des données biologiques. Le modèle statistique doit tenir compte des données biologiques.
On sait très bien que P ("naissance d'un garçon ") > P ("naissance d'une fille")
[mais les filles sont plus résistantes…]
prenons : P (G) = 0.52 et P(F) = 0.48
(Laplace : P (G) = 22/43 = 0,5117 ; anecdote associée à ces statistiques relevés sur 10 ans pour Londres, St Petersburg Berlin et l’ensemble de la France et …25/49=0,5102 pour Paris !)
Sur trois enfants (de mêmes parents),
quelle serait la probabilité d’avoir une seule fille ?
(précision : pas de jumeaux)
4. Exemples
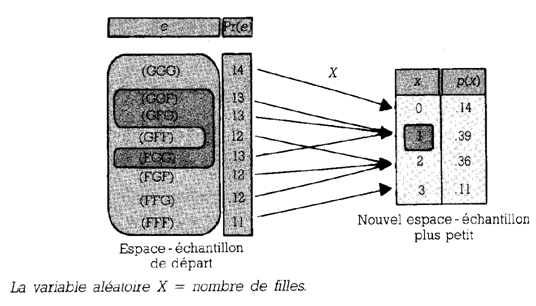
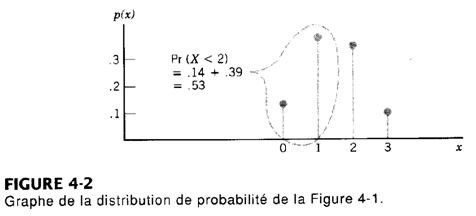
Avec cet exemple nous visualisons :
- variable aléatoire = fonction
- la loi de probabilité
- Calcul de probabilités possible à partir de la distribution
- Nous pouvons calculer la moyenne de la distribution
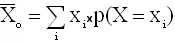
5. Loi Binomiale
La solution du problème des épreuves répétées conduit à la loi binomiale.
On jette 5 fois de suite une pièce de monnaie non truquée.
Quelle est la probabilité d’obtenir 2 fois "face" à l'issue des 5 jets ?
- Quelle est l’épreuve associée ?
- Variable de Bernouilli : pour chaque lancé de la pièce,
Y=0 si le résultat est ‘Pile’ (échec/absence caractéristique) ;
Y=1 si le résultat est face ’Face’ (réussite/présence caractère)
- Echantillon ou population ?
- Variable aléatoire associée ?
- Ensemble des résultats possibles ?
- Quelle est la loi de distribution ?
- Quels sont la moyenne et l'écart-type de la distribution ?
- Représentation graphique
Vers le calcul d’une probabilité : P(X=2)
- Variable aléatoire associée ?
- Résultats possibles
- Généralisation du processus
Commençons par établir la probabilité : P(X=1)
X = 'nombre de 'face' obtenus à l'issue de 5 jets consécutifs d'une pièce non truquée'}
Notons 'P' l'événement 'obtenir pile comme résultat du lancé}
et 'F' l'événement 'obtenir face comme résultat du lancé}
Revue des événements possibles :

Calcul d’une probabilité : P(X=2)

Généralisation du processus : P(X=k)

Triangle de Pascal


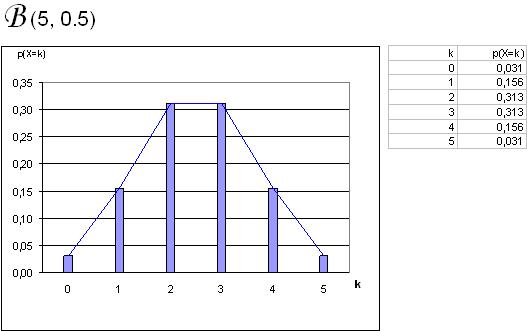
Cas où la loi Binomiale est impliquée :
A chaque fois, qu'une épreuve est répété un certain nombre n de fois (échantillon) avec toujours la même alternative :
un événement E est réalisé (probabilité 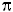 ) ou non réalisé (probabilité 1- ) ou non réalisé (probabilité 1-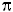 ). ).
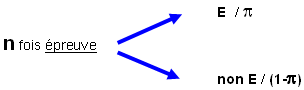
Exemples d'épreuve :
- jet d'une pièce de monnaie
- répondre au hasard à une questions posée
- germination d'une graine
- naissance d'un enfant
- présence d’un résidu d’AA dans une séquence peptidique aléatoire
- etc…
Epreuve, variable et Loi de Bernouilli :
X : variable de Bernouilli, associée à une épreuve possèdant l’alternative :
un événement E est réalisé (probabilité 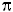 ) ou non réalisé (probabilité 1- ) ou non réalisé (probabilité 1-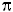 ). ).
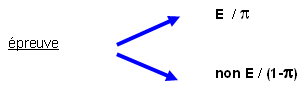
Loi de probabilité :

Loi Binomiale
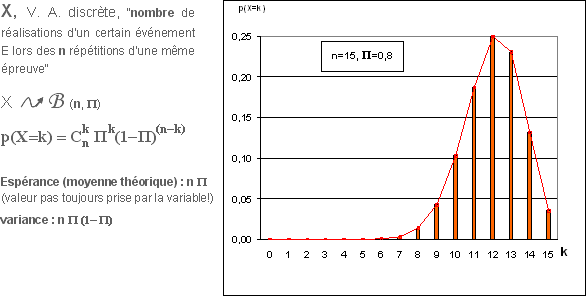
Cependant cette loi est peu pratique à utiliser lorsque n est grand (calculs fastidieux!)
 Tables de la loi binomiale … Tables de la loi binomiale …
 Approche par d'autres lois lorsque c'est possible ... Approche par d'autres lois lorsque c'est possible ...

Loi Binomiale
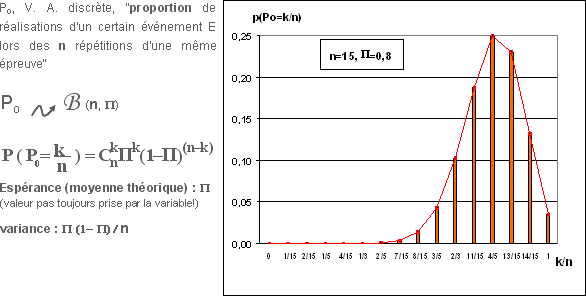

Exercice "Le technicien expérimenté"
Le technicien d’un laboratoire pilote réalise une manipulation très délicate qu’il ne rate que dans 30 % des cas : l’injection d’un fragment d’ADN contenant un gène humain dans le noyau d’un oeuf de souris (étape cruciale pour obtenir des souris transgéniques). Il procède par série de 5 manipulations. Grâce à son expérience, il répète un assez grand nombre de fois ses séries de manipulations dans des conditions pratiquement identiques.
La V.A. d’étude est X = « nombre de manipulations réussies par série de 5 »
Quel est le type de la V.A. X ?
Représentez graphiquement la distribution de X
Quels sont l’espérance et l’écart-type de cette distribution ?
Hypothèse : on supposera sans le démontrer que les manipulations sont toutes indépendantes les unes des autres (effet de la fatigue, impact d’un échec ou d’une réussite sur la manip suivante non pris en compte)
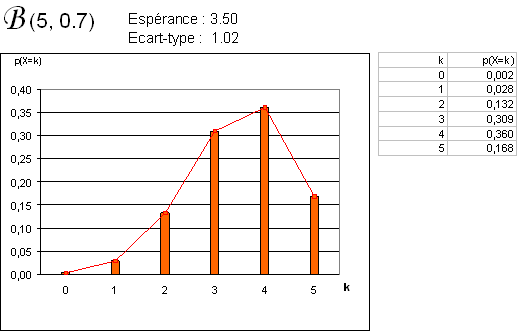
Exercice "sachets de graines"
Un producteur de graines vient de lancer une superbe variété de fleur. Il garantit (sur 1 an) que seules 2 graines sur 10 ne germent pas. Chaque sachet mis en vente contient 200 graines.
a/ Indiquez combien de fleurs peut donner en moyenne un sachet de graines.
b/ Quel est l'écart type associé ?
c/ Pour obtenir un massif de 500 fleurs, combien de sachets faut-il acheter en moyenne ? (Indiquez votre raisonnement).
Vous n'oublierez pas de bien définir la VA sous jacente et d'indiquer sa nature (qualitative, quantitative discrète ou quantitative continue).

Exercice "Séquence Random"
On considère une chaîne polypeptidique de n acides aminés générée de façon aléatoire.
Soit n=50, taille de la séquence
Hypothèse de départ : on considèrera les 20 acides aminés essentiels
Q1 ) Quelle est la probabilité de trouver plus de 50% de résidus proline dans cette séquence aléatoire ?
Q2 ) Quelle est la probabilité de trouver le tripeptide "LLL" dans cette séquence polypeptidique ?
Q3 ) Un poly L , c’est à dire une séquence polypeptidique constituée uniquement du résidu leucine ?
Correction de l' exercice « Séquence Random »
Q1 )
Variable de Bernouilli associée
Présence Proline associée à X=1 ; P(X=1)=1/20
Absence Proline (présence de tout autre aa) associée à X=0 ; P(X=0)=19/20=0,95

Application numérique : utiliser table de la loi binomiale ou ordinateur !
Exemple : en saisissant LOI.BINOMIALE(25;50;0,05;VRAI) dans Excel,
le résultat recherché est le complémentaire à 1 de cette valeur, donc 0
Q2 )
Soit n : nombre de résidus dans la séquence polypeptidique ;
Soit Nt : nombre de tripeptides dans une séquence de n résidus d'acides aminés
Nt = n – 3 +1
Ici : Nt = 50 – 3 +1 = 48
Variable de Bernouilli / Probabilité élémentaire :
Pour chaque tripeptide considéré dans la séquence
Présence de LLL , W=1 P(W=1)=(1/20)³ =0.000125
Absence de LLL , W=0 P(W=0)=1-0.000125=0.999875
Soit la V.A. Y : "nombre de tripeptides LLL dans la séquence aléatoire de 50 résidus d'aa"
Y suit une loi binomiale 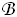 (48, 0.000125) (48, 0.000125)
{Présence de LLL dans la séquence} = (Y > 0)
P (Y > 0) = 1 – P(Y=0)
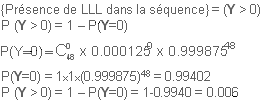

Q3 )
La probabilité recherchée est : (1/20)³ , pratiquement nulle!
Quelques cas où l'on rencontre de la LOI BINOMIALE :
| situation |
variable aléatoire |
nombre de cas |
probabilité de succès sur une épreuve |
hypothèse |
loi de probabilité |
| jet d’une pièce n fois de suite |
X = « nombre de faces obtenues » |
n + 1 possibilités |
 = 0.5 = 0.5 |
pièce non truquée |
Loi binomiale
avec P(X =k)
k appartenant à (0,1,2,...,n)
Variable de Bernouilli :
Succès : Y=0
Echec : Y=1 |
| nombre de filles dans une famille de 8 enfants |
X = « nombre de filles dans un échantillon de 8 enfants
Y = « nombre de garçons» |
{ 0 ; 1 ; .. ; 8} |
P(F) = P(G) = 0.5 |
pas de variation de cette probabilité avec le rang de la naissance |
Loi binomiale
avec P(X =k)
k appartenant à (0,1,2,...,8) |
| questions posées à un examen QCS :
20 questions, 5 propositions par question |
note obtenue sur 20 |
0 => 20
21 notes possibles |
 = 0.2 = 0.2 |
réponse juste
= 1 point
(une seule réponse est bonne et les questions sont indépendantes) |
Loi binomiale
avec P(X =k)
ex : obtenir la moyenne en répondant au hasard au question :
P(X > 10) |
| contrôle qualité d’un échantillon de 10 pipettes au hasard d’une production de 40000 pour lesquelles 32000 sont bonnes |
X = « nombre de pipettes défectueuses» |
0 à 10 pipettes défectueuses |
 = 0.8
(à peu près constante quand n est grand) = 0.8
(à peu près constante quand n est grand)
|
On n'est pas dans un cas d’indépendance
Formelle => on considère la probabilité de l'évènement à 3 chiffres après la virgule. |
On décide tout de même avec une faible erreur de traiter le problème en utilisant la loi binomiale
avec P(X =k), k appartenant à
{ 0,1,2,...,10 } |
6. Loi de Poisson
Exemple introductif
Dans des tests labos faits sur des rats, l’étalement sur la peau d’une crème de soin du commerce peut provoquer une rougeur dans 20 cas sur 1000.
Soit X la variable aléatoire "Nombre de rats présentant une rougeur après dépôt du produit sur N individus"
A/ Quelle loi de probabilité suit X ?
B/ Quelle est la probabilité d'observer moins de 3 cas de réaction sur 100 étalements ?
En déduire la probabilité d'observer au moins 3 cas de réaction sur 100 étalements.
Que constatons-nous dans cet exemple ?
X suit une loi binomiale dont la moyenne est très proche de la variance
Et P petite pour N plutôt grand => évènement rare
Moyenne : n = 0.02*100 = 2 = 0.02*100 = 2
Variance : n (1- (1- ) = 100*0.02*0.98 = 1.96 ) = 100*0.02*0.98 = 1.96
Cas d'application (Siméon Denis Poisson 1781-1840)
Lorsque le nombre d'épreuves n est grand et  très petit (proche de 0) très petit (proche de 0)
la loi Binomiale 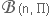 tend vers une loi de Poisson tend vers une loi de Poisson 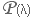 de seul paramètre de seul paramètre 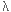 (espérance et variance de la loi binomiale approchée par la loi de Poisson).
La loi de Poisson est une distribution discrète. Elle est tabulée (espérance et variance de la loi binomiale approchée par la loi de Poisson).
La loi de Poisson est une distribution discrète. Elle est tabulée
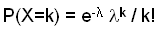
Côté pratique
On vérifiera d'abord que les calculs ne peuvent être approchés par une distribution normale, plus pratique à utiliser
Nous sommes maintenant armés pour résoudre notre exemple introductif
Dans une expérience faite sur des rats, l’étalement sur la peau d’une crème de soin du commerce peut provoquer une rougeur dans 20 cas sur 1000.
Soit X la variable aléatoire "Nombre de rats présentant une rougeur après dépôt du produit sur N individus"
A/ Quelle loi de probabilité suit X ?
B/ Quelle est la probabilité d'observer moins de 3 cas de réaction sur 100 étalements ?
En déduire la probabilité d'observer au moins 3 cas de réaction sur 100 étalements.
On va utiliser une loi de Poisson de paramètre 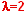
Et si on le faisait avec R ? ...
Fonction : dpois
Réels domaines d’utilisation d’une loi de Poisson
 Nombre d’évènements par unité de volume, de surface, de temps Nombre d’évènements par unité de volume, de surface, de temps
- Nombre de poissons par mètres cube d’eau
- Passages d’un ours dans un site des Pyrénées sur une semaine
- Concentration de bactéries (hématimètre) dans un lac (homogénéité)
- Nombre d’insectes d’une certaine espèce capturés sur un filet en une nuit en forêt amazonienne
- Nombre de désintégration d’un radio-isotope par minute
- Nombre d’appels enregistrés par un standard téléphonique dans une courte période de temps
- Nombre de skieurs empruntant un télésiège en l’espace d’une heure dans une petite station alpine
- etc.
Exercice "les ours des Pyrénées"
Un écologiste étudie le passage des ours (récemment introduits) en un point précis d’une rivière séparant un champ d’une petite forêt des Pyrénées. A l’issue d’un travail long (plusieurs semaines) et rigoureux, il observe en moyenne 4 individus par jour.

7. Calcul de probabilités dans le cas des lois de distribution continues
Transformation de l'échelle verticale des graphes
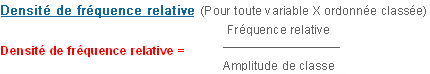
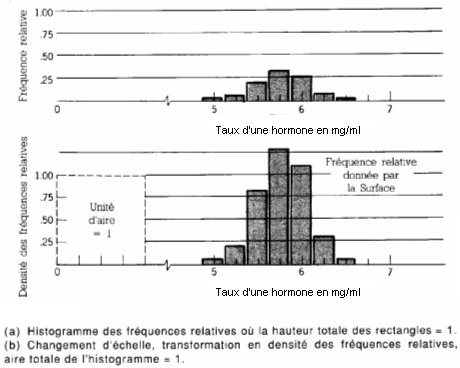
Avec la densité de fréquence relative on a facilement accès aux probabilités, associées aux surfaces du diagramme.
AIRE TOTALE = 1
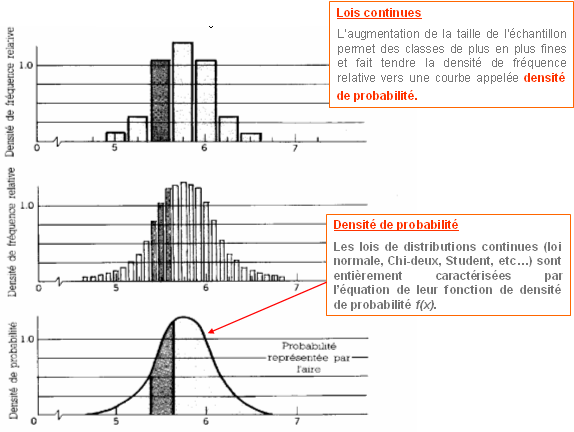
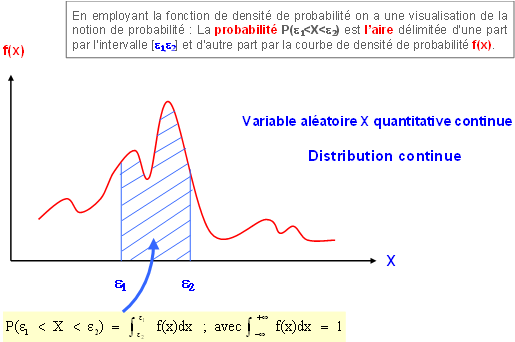
Remarques

8. Loi Normale
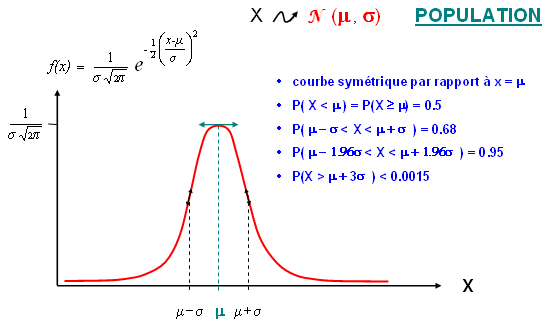
De nombreuses variables aléatoires ont pour fonction de densité une courbe en forme de cloche, appelée courbe Normale ou courbe de Laplace-Gauss (Pierre Simon de Laplace 1749-1827 ; Karl Friederich Gauss 1777-1855)
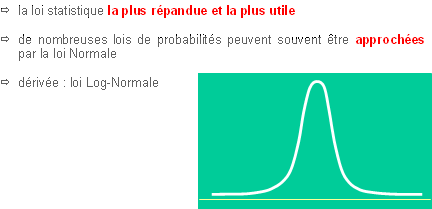
Loi de Laplace-Gauss quand est-elle rencontrée ?
Lorsqu'une grandeur subit l'influence d'un grand nombre de facteurs (ou paramètres ; non tous identifiés, voire identifiables!) tous indépendants, qui, pris isolément, ne contribuent que très faiblement à faire varier la grandeur étudiée, les valeurs prises par la variable aléatoire (continue) associée à la grandeur se distribuent selon la loi de Laplace-Gauss (appelée Loi Normale). Cette loi revêt un caractère de généralité. On y fait très souvent appel en Biologie

- Propriétés de la Loi Normale N (m, s) , repères graphiques
- Définition des fonctions de densité de probabilité et de partition
- Une probabilité est une aire (comme pour toute distribution continue)
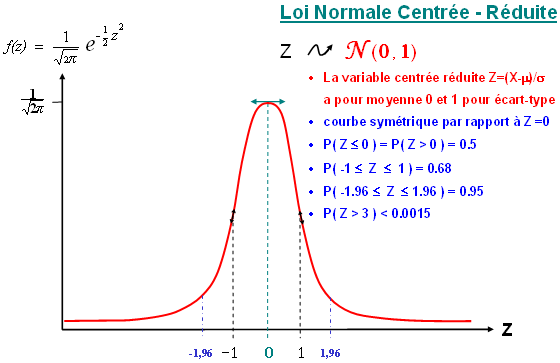
- Loi Normale centrée réduite
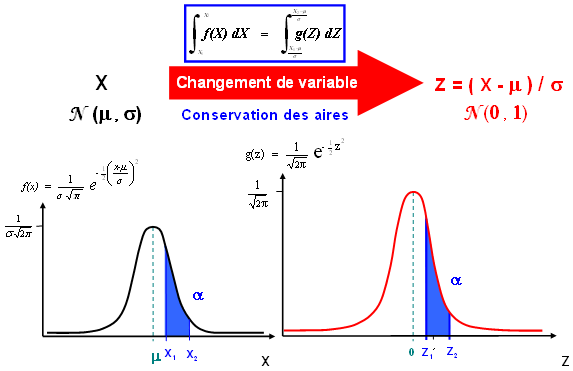
- Changement de variable et conservation des aires
- Lecture des tables de la Loi Normale centrée réduite
- Un exemple
- Bilan de ce qu’il faut retenir
- Exercices
- Loi Log-Normale
- Passage d’une loi Binomiale à une loi Normale
Principe de la table de la loi Normale Centrée Réduite
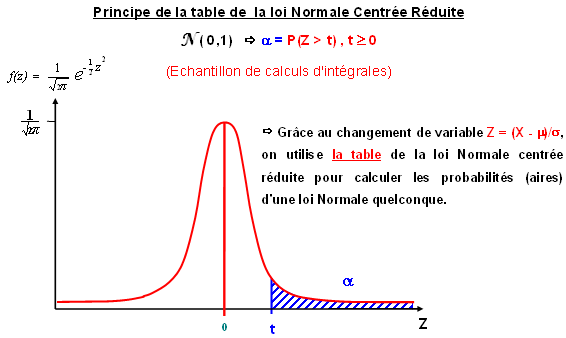
 Grâce au changement de variable Grâce au changement de variable  , on utilise la table de la loi Normale centrée réduite pour calculer les probabilités (aires) d'une loi Normale quelconque. , on utilise la table de la loi Normale centrée réduite pour calculer les probabilités (aires) d'une loi Normale quelconque.
Table de la loi Normale Centrée Réduite

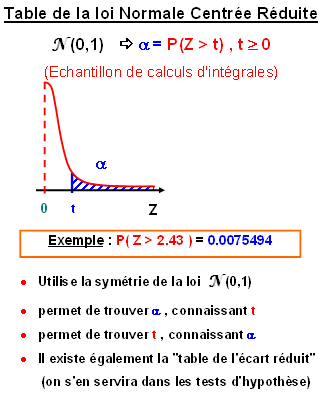
Du Côté d’EXCEL :
(loi normale quelconque)
- loi.normale renvoie la valeur de P(X < z) pour z donné
- loi.normale.inverse renvoie z à partir de P(X < z)
Exercice "Les grains de maïs"
Les ingénieurs d'une coopérative agricole ont constaté que les grains d'un maïs issus d'une sélection (résistant mieux aux intempéries) sont moins lourds que ceux du maïs utilisé jusqu'alors par la coopérative. Suite à des statistiques répétées sur plusieurs années, on note que la masse des grains est distribuée normalement dans les 2 populations de maïs, avec pour moyennes et écart-type exacts :
- maïs utilisé par la coopérative => moyenne : 3,4 g ; écart-type : 0,5 g
- variété sélectionnée pour sa résistance aux intempéries => moyenne : 3,2 g ; écart-type : 0,5 g
Seuls les grains de masse supérieure à 2,5 g sont commercialisables
A/ Calculez la probabilité des évènements suivants, d'une part pour le maïs utilisé par la coopérative,
d'autre par pour le maïs sélectionné :
- La masse des grains est inférieure à 2,5 g
- La masse des grains est comprise entre 3,0 et 4,0 g
- La masse des grains est supérieure à 4,0 g
B/ On prélève au hasard un grain de chacun des 2 types de maïs, quelle est la probabilité qu'un grain de
maïs utilisé par la coopérative ait une masse supérieure à celui du maïs sélectionné ?
C/ On dispose de données complémentaires qui montrent le traitement par un produit K translate les
distributions de 100 mg sur la gauche.
- Quelle est la proportion de grains non commercialisables chez le maïs exposé au traitement K et
chez le maïs non exposé au traitement K ?
- Quelle est l'augmentation relative du risque de non-commercialisation chez le maïs exposé au *
traitement K par rapport au maïs non exposé ?
Rappels occasionnés par l’exercice
Propriétés de l'espérance et de la variance
L'espérance, ou moyenne, d'une somme de variables aléatoires est égale à la somme des espérances de ces variables => E(X1+ X2 + ... + Xn) = E(X1) + E (X2) + ...+ E(Xn)
La variance d'une somme, doit tenir compte du facteur covariance :
Var(X+Y) = Var(X) + Var(Y) + 2 cov(X,Y), avec cov(X,Y) = E(XY) – E(X).E(Y)
Toutefois, si X et Y sont 2 VA indépendantes, cov(X,Y) = 0 et dans ce cas : Var(X+Y) = Var(X) + Var(Y).
Coefficient de corrélation
La covariance de 2 variables X et Y dépend des unités choisies pour mesurer X et Y (par ex, lorsque X est exprimé en Molaire tandis que Y l’est en mili-Molaire, cela induit un facteur 1000). Pour s’affranchir de ce problème, on utilise un coefficient (noté p) très pratique, le coefficient de corrélation de X et de Y défini par 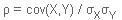
9. Passage d'une loi binomiale à une loi normale
Evolution de la forme d'une distribution binomiale lorsque n est grand
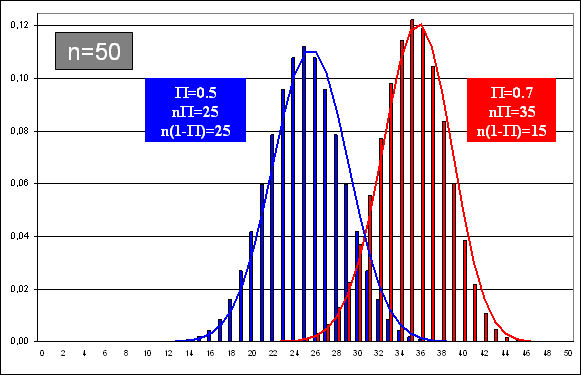
Pratique : Les calculs impliquant une distribution binomiale peuvent,
dans certains cas, être approchés par une distribution normale (plus pratique à utiliser)
 On utilise la moyenne et l’écart-type de la Binomiale pour définir la Normale On utilise la moyenne et l’écart-type de la Binomiale pour définir la Normale


Exercice "Kit ou … double?"
L'industriel fabricant des kits de biotechnologie a mis en place une technique éliminant les éléments défectueux. A l'issue de cette étape, 99% des kits vendus sont corrects et utilisables sans risque de disfonctionnement.
L'industriel vient juste de vendre un lot de 1000 kits à l'un de ses distributeurs. Préoccupé par son image de marque, il a demandé à une jeune stagiaire de lui donner, dans l'heure, la probabilité qu'il y ait plus de 2% de kits défectueux dans le lot vendu.
Qu'en serait-il s'il avait vendu :
- un lot de 10000 kits?
- un lot de 100 kits?
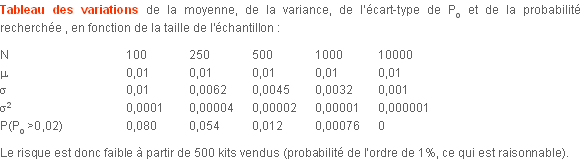
Tracez les variations de la variance en fonction de la taille de l'échantillon
Définissons les variables aléatoires utilisables dans cet exercice,
X = « Nombre d’éléments défectueux dans un lot de N kits de biotechnologie vendus »
 = « Proportion d’éléments défectueux dans un lot de N kits de biotechnologie vendus » = « Proportion d’éléments défectueux dans un lot de N kits de biotechnologie vendus »
L’épreuve de Bernoulli, répétée N fois, associe la probabilité  =1-0,99=0,01 (paramètre) à l’évènement « un kit pris au hasard est défectueux ». =1-0,99=0,01 (paramètre) à l’évènement « un kit pris au hasard est défectueux ».
L'industriel vient juste de vendre un lot de 1000 kits à l'un de ses distributeurs. N=1000
X suit la loi binomiale B(1000, 0,01) de moyenne N =10 =10
 suit la loi binomiale B(1000, 0,01) de moyenne suit la loi binomiale B(1000, 0,01) de moyenne  =0,01 =0,01
et d’écart type [ (1- (1- )/N]½ =[0,01x0,99/1000]½=0,0032 )/N]½ =[0,01x0,99/1000]½=0,0032
P(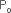 >0,02) = P(X>20) = 1-[P(X=0)+P(X=1)+...+P(X=20)]. Ce calcul impliquant la somme de 21 termes binomiaux est bien trop fastidieux. On s’intéresse donc de suite sur l’approximation par une loi Normale. Comme N >0,02) = P(X>20) = 1-[P(X=0)+P(X=1)+...+P(X=20)]. Ce calcul impliquant la somme de 21 termes binomiaux est bien trop fastidieux. On s’intéresse donc de suite sur l’approximation par une loi Normale. Comme N et N(1- et N(1- ) sont tous deux supérieurs à 5, cette approximation est possible.
Soit Y la variable aléatoire suivant la loi normale N( ) sont tous deux supérieurs à 5, cette approximation est possible.
Soit Y la variable aléatoire suivant la loi normale N( , [ , [ (1- (1- )/N]1/2), les fluctuation de )/N]1/2), les fluctuation de 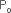 peuvent être approchées par la loi de Y. Pour N=1000 et peuvent être approchées par la loi de Y. Pour N=1000 et  =0,01, Y suit la loi N(0,01, 0,0032) =0,01, Y suit la loi N(0,01, 0,0032)
P(Po>0,02)=P(Y>0,02)
P(Y>0,02)=P[Z>(0,02-0,01)/0,0032)], Z suivant la loi normale centrée réduite N(0,1)
P(Y>0,02)=P(Z>3,17)
P(Z>3,17)=0,00076
Ainsi la probabilité recherchée P( >0,02) est proche de 0,08%. L’industriel peu se rassurer ! >0,02) est proche de 0,08%. L’industriel peu se rassurer !
S'il avait vendu un lot de 10000 kits, l’approximation Normale est encore meilleure. La moyenne ne change pas, elle est toujours égale à 0,01 mais l’écart type de la loi B(1000, 0,01) valant [0,01x0,99/10000]1/2=0,000995 (à peu près 0,001), la position de la valeur 0,02 sur la distribution normale est cette fois à plus de 10 écart-type de la position de la moyenne 0,01 ! Autrement dit la probabilité recherchée est nulle.
S'il avait vendu un lot de 100 kits,
N =1, étant inférieur à 5, l’approximation Normale n’est cette fois plus possible.
La moyenne de la loi B(100, 0,01) suivie par X vaut N =1, étant inférieur à 5, l’approximation Normale n’est cette fois plus possible.
La moyenne de la loi B(100, 0,01) suivie par X vaut N =1 et la variance est 0,01x0,99x100=0,0099, valeur très proche de la moyenne. On ne peut donc utiliser la loi de Poisson P(1), de paramètre =1 et la variance est 0,01x0,99x100=0,0099, valeur très proche de la moyenne. On ne peut donc utiliser la loi de Poisson P(1), de paramètre 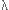 =1 pour effectuer les calculs.
Attention, N=100 donc P( =1 pour effectuer les calculs.
Attention, N=100 donc P(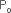 >0,02) = P(X>2) >0,02) = P(X>2)

10. Some more training
Exercice : "Les citrons" (extrait de l’examen 2002)
Des citrons sont produits dans des conditions reproductibles par une entreprise agroalimentaire du sud de l’Espagne pour laquelle vous travaillez. Ces citrons forment une population de référence. Leur diamètre est distribué normalement dans cette population avec une moyenne de 7,0 cm et un écart-type de 1,0 cm.
Un dispositif performant permet également de détecter, sur chaque citron, la concentration de pesticide absorbé par l'écorce. Cette grandeur est, elle aussi, distribuée normalement dans la population référence avec une moyenne de 2,5 mg/ml et un écart-type de 0,2 mg/ml.
Les citrons sélectionnés pour la vente sont ceux dont le diamètre (*) est compris entre 5,5 et 9,0 cm (inclus) et dont la concentration de pesticide absorbé par l'écorce est inférieure ou égale à 2,8 mg/ml
Calculez
la proportion de citrons sélectionnés pour la vente dans la population référence.
(* Les citrons trop petits n’intéressent personne tandis que les citrons trop volumineux ont une écorce trop épaisse et, très souvent, une forme irrégulière déplaisant aux consommateurs).
Population référence : citrons produits dans des conditions reproductibles par la firme agroalimentaire (population infinie).
Soit X la variable aléatoire (quantitative continue) : "diamètre des citrons en cm" ;
X suit une loi N (7,0, 1,0)
Soit Y la variable aléatoire (quantitative continue) :
" concentration de pesticide absorbée par l'écorce d'un citron en mg/ml" ;
Y suit une loi N (2,5, 0,2)
a/ La proportion de citrons sélectionnées pour la vente dans la population référence (population infinie) correspond à la probabilité 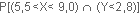 ; ;
les 2 variables X et Y étant indépendantes :

Exercice "Diamond is the best girl friend ..."
Tous les ans, le groupe agro-alimentaire DIAMOND (23 usines en Europe) est confronté à une dure réalité : sur cinq réacteurs de la gamme R201 contrôlés, trois en moyenne ont besoin d'une sérieuse révision. Une révision est facturée 500 Euros HT par réacteur.
L'usine de Toulouse possède 11 réacteurs de la gamme R201.
1/ Quelle est la probabilité que la facture de la révision de ses réacteurs soit comprise entre 1000 et 1500 Euros HT ?
2/ Quelle est la probabilité qu'elle soit supérieure ou égale à 1500 Euros HT ?
3/ Quel est le coût moyen des réparations ?
Pour répondre aux questions :
Définissez la population et l'échantillon d'étude.
Vous allez être amenés à utiliser 2 variables aléatoires. Définissez ces 2 variables. Pour chacune d'elles, vous indiquerez si elle est discrète ou continue.
Justifiez vos calculs d'1 ou 2 lignes de commentaires en français.
Population : tous les réacteurs en service dans les 23 usines européennes du groupe agro-alimentaire
Echantillon : les 11 réacteurs de l'usine de Toulouse
Posons X=« Nombre de réacteurs ayant besoin d’une révision dans un échantillon de 11 »
X , variable quantitative discrète, suit une B(11,3/5) ;  =0,6 =0,6
Appelons R le coût HT d’une réparation. R = 500 euros.
Posons Z=« Coût des réparations à réaliser dans l’usine de Toulouse »
Z=R.X, avec R constante

Exercice : "Du tabac pour la bonne cause"
Des études menées sur une exploitation pilote ont montré que la quantité d’une protéine recombinante produite par un pied de tabac peut être représentée par un variable normale de moyenne 10 mg et d’écart-type 2 mg.
Quelle est, dans ces conditions, la probabilité d’observer dans cette exploitation un plan ayant produit plus de 13 mg de protéine ?
On prélève au hasard 50 plans de tabac de l’exploitation pilote.
Quelle est la probabilité d’observer au moins 3 plans ayant produit chacun plus de 15 mg de la protéine recombinante?
- Commentez ces résultats
Il est conseillé de bien définir la VA et la loi suivie par la VA pour répondre aux questions, de faire un schéma si possible.
Posons X =« quantité en mg d’une protéine recombinante produite par un pied de tabac »
X suit la loi N(10, 2). Nous recherchons P(X>13).
P(X > 13) = P[Z >(13-10)/2] , Z suivant la loi normale centrée réduite N(0, 1).
P(X > 13) = P[Z > 1,5]
P(X > 13) = 0,06681 , soit 7% environ, ce qui n’est donc pas négligeable.
Posons Y =« nombre de plans de tabac produisant plus de 15 mg de protéine recombinante parmi les 50 plans récoltés»
Y suit la loi binomiale B(50, P(X > 15)). Il faut au préalable déterminer P(X > 15).
P(X > 15) = P[Z > (15-10) /2] ; P(X > 15)=P[Z > 2,5] = 0,0062
Ainsi, plus précisément, Y suit donc une binomiale B(50, 0,006).
On recherche P(Y = 3)=P(Y>2)=1-P(Y = 2)
P(Y = 3) = 1-[P(Y=0)+P(Y=1)+P(Y=2)]
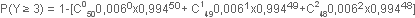
Nous remarquons immédiatement que la probabilité associée à l’épreuve de Bernoulli (probabilité élémentaire) est très petite. Ce qui laisse espérer l’utilisation d’une loi de Poisson.

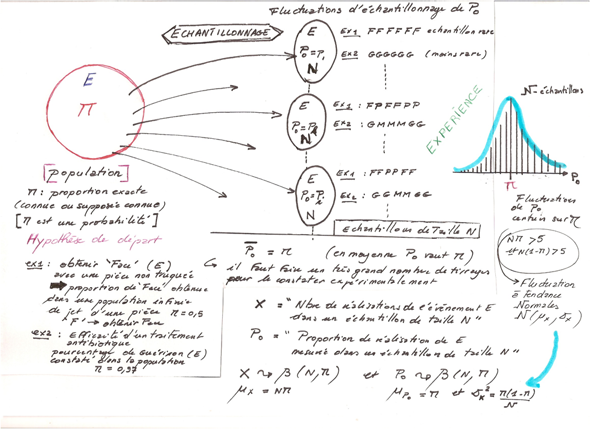
11. Fluctuation d'échantillonage d'une proportion expérimentale (observée)
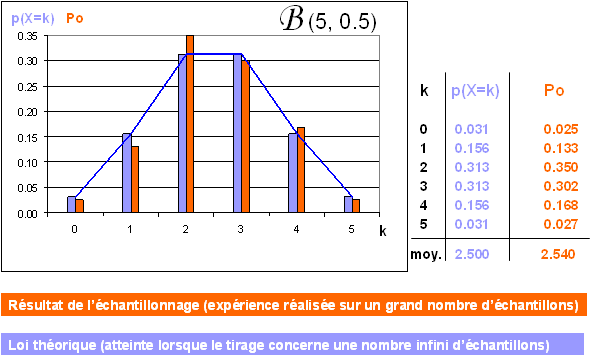
12. Travail avec R
Travail demandé :
Résoudre tous les exercices proposés en cours avec le logiciel R
(Un bon entraînement pour les examens pratique et théorique) |