|
E - Inférence statistique
1. Introduction - Déduction et inférence statistique
2. Fluctuations d'échantillonnage d'une proportion observée
3. Principe et résolution d'un test d'hypothèse
4. Fluctuations d’échantillonnage d’une moyenne observée
5. Comparaison de 2 variances observées / de 2 moyennes observées
6. Tests du Khi-deux (non paramétrique)
1. Introduction - Déduction et inférence statistique
Population : ensemble total d'objets ou d'individus à étudier, à partir duquel sont extraits des échantillons.
La moyenne µ et l'écart-type σ de la population sont des constantes (généralement inconnues), exemple de paramètres fixes de la population ou objectifs.
 Les probabilités P(X) sont utilisées dans le calcul de σ et µ Les probabilités P(X) sont utilisées dans le calcul de σ et µ
Echantillon : Sous ensemble de la population. Un échantillon représentatif est un sous-ensemble choisi au hasard dans la population.
La moyenne 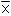 et l'écart-type s de l'échantillon sont des variables aléatoires, variant d'un échantillon à l'autre, et sont appelées statistiques d'échantillon, statistiques aléatoires ou estimateurs ici respectivement (µ et σ) et l'écart-type s de l'échantillon sont des variables aléatoires, variant d'un échantillon à l'autre, et sont appelées statistiques d'échantillon, statistiques aléatoires ou estimateurs ici respectivement (µ et σ)
Remarque : la médiane 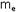 peut être dans certains cas un meilleur estimateur de µ que peut être dans certains cas un meilleur estimateur de µ que 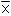
Les fréquences relatives f/n sont utilisées dans le calcul de 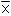 et de s. et de s.
 [ Un estimateur T est dit biaisé si son espérance E(T) est différente de sa cible [ Un estimateur T est dit biaisé si son espérance E(T) est différente de sa cible  dans la population : dans la population :
biais = E(T)- ] ]
Tirage d'un échantillon avec remise : important pour garantir l'indépendance de n observations qui le constituent (surtout dans les petites populations).
La proportion comme la moyenne changeant sinon à chaque tirage !
Tirage d'un échantillon sans remise : sans importance dans les grandes populations, aucune différence pratiquement que l'on remette ou non chaque individu avant le tirage suivant. Pour l'essentiel les observations sont indépendantes. Ce n'est pas le cas pour une petite population.
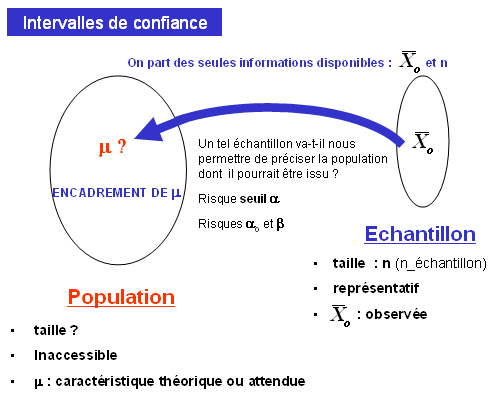
Déduction : prédire, à partir d'une population connue ou supposée connue, les caractéristiques des échantillons qui en seront prélevés.
Induction (inférence) : prédire les caractéristiques d'une population inconnue à partir des statistiques déterminées dans un échantillon représentatif de cette population.
 Extrapolation des observations réalisées dans un échantillon à l'ensemble de la population. Extrapolation des observations réalisées dans un échantillon à l'ensemble de la population.
Allons-y ...
- Etude des fluctuations d'échantillonnage d'une proportion observée
- Tests d'hypothèses (conformité, homogénéité)
- Estimations : intervalles de pari, intervalles de confiance
- Etude des fluctuations d'échantillonnage d'une moyenne observée (en se servant du modèle de cahier des charges vu lors de l'étude des flucuations d'échantillonnage d'une proportion observée)
- Intervalles de pari, Intervalles de confiance
- Autre test utile : Test du
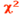 de Pearson , (tests : conformité, homogénéité, ajustement à une loi) de Pearson , (tests : conformité, homogénéité, ajustement à une loi)
- Exemples, exercices
- IMPORTANCE DES SCHéMAS !
Tests d'hypothèses
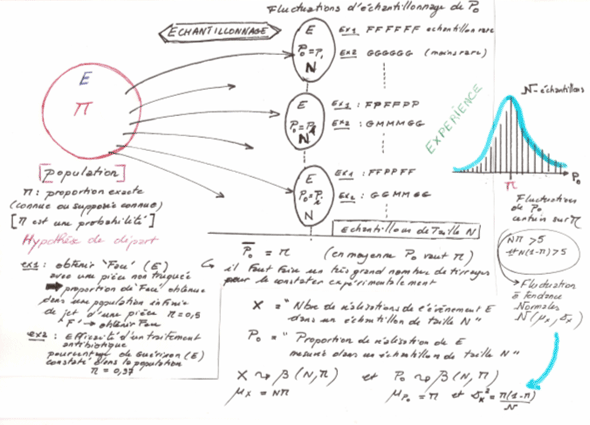
2. Fluctuations d'échantillonnage d'une proportion observée
Les proportions, indicateurs parmi d'autres
- Définition
- Intérêt
- On travaille sur un échantillon de taille quelconque pour obtenir des informations sur la population d’origine
- Caractéristique : II [population]
- Statistique :
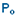 [observée ou observable sur un n-échantillon] [observée ou observable sur un n-échantillon]
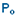 comme estimateur de II comme estimateur de II- Tests et encadrements possibles : sur II et
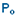
- On va travailler sur le biais :
 = =  - - 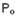
Comment traduire P(X=k)=0.33 ?
 Si l’on répétait un très grand nombre de fois l’expérience on obtiendrait X=k dans 33% des cas Si l’on répétait un très grand nombre de fois l’expérience on obtiendrait X=k dans 33% des cas
 Autre façon de le formuler : 33% des échantillons conduisent à X=k (nbre infini de tirages) Autre façon de le formuler : 33% des échantillons conduisent à X=k (nbre infini de tirages)
En remplaçant X=k par Po= k/n :
 Fluctuations d’échantillonnage d’une proportion observée. Fluctuations d’échantillonnage d’une proportion observée.
 Nature : Loi Binomiale de paramètres n et (objectif dans population) Nature : Loi Binomiale de paramètres n et (objectif dans population)
 Problème continu lorsque n très grand. Problème continu lorsque n très grand.
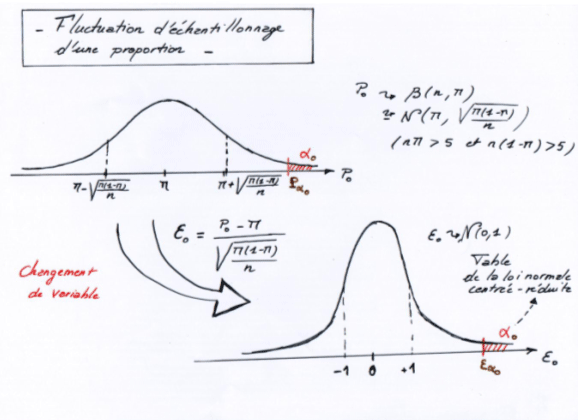
Fluctuations d'échantillonnage d'une proportion observée
 Le caractère étudié est qualitatif et sa répartition dans l'échantillon ou la population constitue une variable aléatoire quantitative discrète. Le caractère étudié est qualitatif et sa répartition dans l'échantillon ou la population constitue une variable aléatoire quantitative discrète.
Lorsqu'un évènement donné E a une probabilité II d'être observée dans une population, la proportion observée 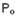 de cet évènement dans n-échantillons, tirés au hasard de la population, subit des fluctuations d'échantillonnage suivant une loi binomiale de moyenne II et d'écart-type de cet évènement dans n-échantillons, tirés au hasard de la population, subit des fluctuations d'échantillonnage suivant une loi binomiale de moyenne II et d'écart-type 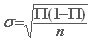
En pratique (ceci rend les calculs de probabilité aisés)

Alors la loi binomiale est approchée par une loi Normale de même moyenne et même écart-type
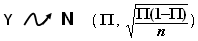
Nous seront amenés à vérifier cette condition à priori ou à posteriori !
 Nous allons exploiter ces propriétés Nous allons exploiter ces propriétés
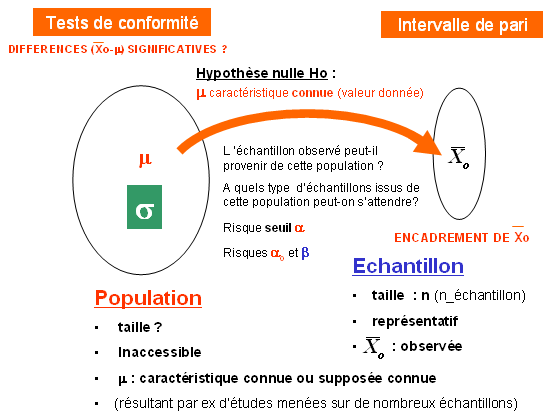
Une intervalle de pari, au risque (ou taux, ou seuil) α,
encadre les valeurs de 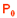 , observables dans un n-échantillon lorsque celui-ci est tiré au hasard d'une population caractérisée par le paramètre exact II , observables dans un n-échantillon lorsque celui-ci est tiré au hasard d'une population caractérisée par le paramètre exact II
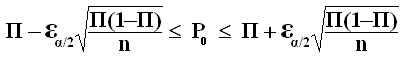
Poser l'hypothèse nulle (dotée Ho)
La probabilité de trouver 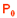 dans cet intervalle est (1-α) dans cet intervalle est (1-α)
Seuil standard : α = 5%
Il faut, bien sûr, être dans une situation où l'on peut approcher les fluctuations binomiales de la variable d'échantillonnage 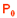 par une loi normale. par une loi normale.
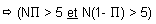
Important : on considère 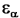 dans la table de l'écart réduit dans la table de l'écart réduit
mais 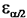 dans la table N(0,1) plus précise dans la table N(0,1) plus précise
Tirage aléatoire d'échantillons issus d'une population caractérisée par le paramètre 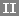
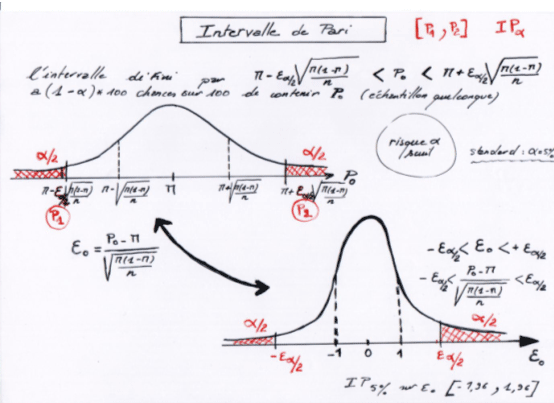
Grâce à la distribution normale, on peut trouver aisément les deux bornes de l'intervalle centrée sur 
Exercice "La machine déréglée"
La production d'une machine déréglée conduit à 50% de pièces défectueuses.
Un échantillon de 100 pièces est extrait de la production de cette machine.
- Quelle est la probabilité d'observer moins de 30% de pièces défectueuses dans l'échantillon ?
- L'une des personnes travaillant à l'atelier voisin a parié un iPhone que la proportion observée de pièces défectueuses est comprise entre 40% et 60%. Quel risque a-t-elle pris de perdre son pari ?
- Déterminer l'IP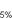 de cette proportion de cette proportion
- Quelle(s) fonction(s) peux-on utiliser pour faire ces calculs avec R ?
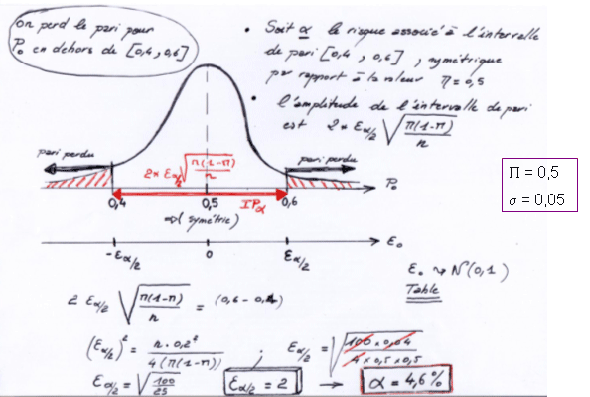
probabilité d’observer entre 40% et 60% de pièces défectueuses dans l’échantillon : 95,4 %
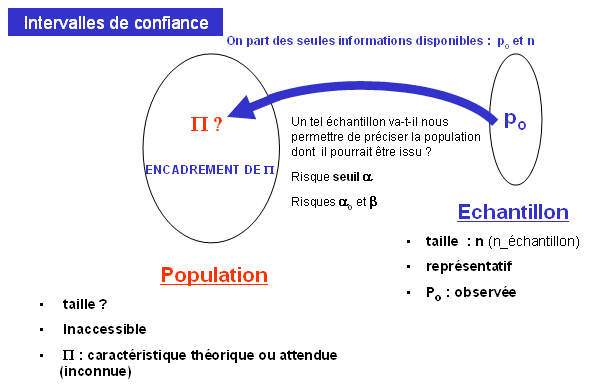
Intervalle de confiance (IC ) : intervalle encadrant les valeurs de II permettant de caractériser un ensemble de populations dont pourrait être issu l'échantillon dans lequel la valeur ) : intervalle encadrant les valeurs de II permettant de caractériser un ensemble de populations dont pourrait être issu l'échantillon dans lequel la valeur  a été observée. a été observée.
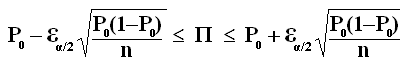
Validation de l'IC : il faut finalement vérifier à posteriori que nII et n(1-II) sont tous deux supérieurs à 5 aux deux bornes de l'intervalle. Dans le cas contraire, on ne peut pas valider l'intervalle de confiance. : il faut finalement vérifier à posteriori que nII et n(1-II) sont tous deux supérieurs à 5 aux deux bornes de l'intervalle. Dans le cas contraire, on ne peut pas valider l'intervalle de confiance.
Important : on considère 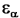 dans la table de l'écart réduit dans la table de l'écart réduit
mais 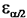 dans la table N(0,1) plus précise dans la table N(0,1) plus précise
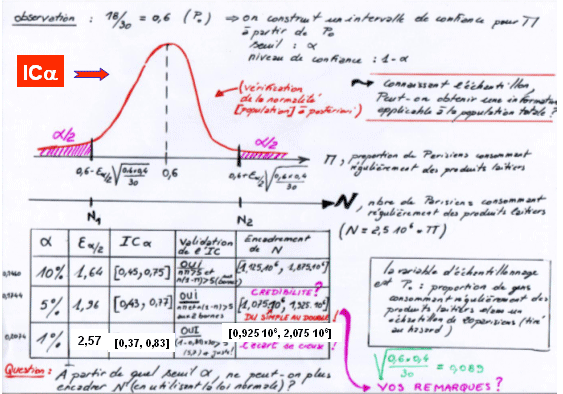
Exercice "Les produits laitiers"
Un micro sondage a révélé que sur 30 parisiens interrogés au hasard dans la rue, 18 consomment régulièrement des produits laitiers (lait, fromages, yaourts, beurre, produits dérivés du lait ...). En sachant que la ville de Paris compte 2,5 millions d'habitants, estimez le nombre de parisiens consommant régulièrement des produits laitiers aux risques de 10%, 5% et finalement 1% ?
Quels sont vos commentaires?
3. Principe et résolution d'un test d'hypothèse
Cette partie va nous permettre de développer le principe des tests d’hypothèses et de présenter la méthode de résolution des problèmes qui leurs sont associés.
Généralités
Les tests sur les proportions vont servir de modèles pour tous les tests d’hypothèses.
Pour résoudre un test d’hypothèses il va falloir suivre une procédure.
Cette méthode permet d’obtenir toutes les conclusions que l’on peut tirer des observations dont on dispose, conclusions pouvant servir de base à une décision.
Il n’y a jamais de réponse absolue dans cette démarche !
Les conclusions des tests d’hypothèse doivent faire apparaître les risques de se tromper qui y sont associés (en termes de probabilités)
Avertissement
Tirer des conclusions à partir d ’un nombre limité d’observations (échantillon).
 La certitude absolue ne peut jamais être atteinte car la population totale n’est connue qu’à travers l’image imparfaite que constitue l’échantillon.
Mais le degré de confiance que l’on peut accorder à une conclusion peut être formulée en terme de probabilité. La certitude absolue ne peut jamais être atteinte car la population totale n’est connue qu’à travers l’image imparfaite que constitue l’échantillon.
Mais le degré de confiance que l’on peut accorder à une conclusion peut être formulée en terme de probabilité.
Posons la problématique
Une observation faite sur un échantillon semble peu probable dans la population référence (ou incompatible avec un autre échantillon) ...
 Les écarts constatés entre l'échantillon et la population totale sont-ils significatifs ou imputables au hasard des fluctuations d'échantillonnage ? Les écarts constatés entre l'échantillon et la population totale sont-ils significatifs ou imputables au hasard des fluctuations d'échantillonnage ?
 On confronte la loi suivie dans la population à la probabilité de l'observation dans un échantillon tiré au hasard de la population. On est ainsi amené à poser une hypothèse (dite hypothèse nulle) pouvant rendre compte de cette observation. On confronte la loi suivie dans la population à la probabilité de l'observation dans un échantillon tiré au hasard de la population. On est ainsi amené à poser une hypothèse (dite hypothèse nulle) pouvant rendre compte de cette observation.
 L'approche est la même pour toutes les variables d'échantillonnage étudiées (proportion, moyenne ...) et pour tous les tests d'hypothèses (tests de conformité, d'homogénéité, dajustement à une loi de distribution) et toutes les lois de distribution utilisées (loi normale, Student-Fisher, Chi-Deux ...). L'approche est la même pour toutes les variables d'échantillonnage étudiées (proportion, moyenne ...) et pour tous les tests d'hypothèses (tests de conformité, d'homogénéité, dajustement à une loi de distribution) et toutes les lois de distribution utilisées (loi normale, Student-Fisher, Chi-Deux ...).
 Décision : rejet ou non de l'hypothèse nulle ; différences significatives ou dues au hasard des fluctuations d'échantillonnage. Décision : rejet ou non de l'hypothèse nulle ; différences significatives ou dues au hasard des fluctuations d'échantillonnage.
Si les tests permettent de réfuter une hypothèse nulle avec un degré de confiance parfaitement défini, ils sont, dans l'autre sens, impuissants à démontrer la satisfaction de l'hypothèse nulle ; ils indiquent simplement que celle-ci n'est pas contredite par les faits.
Quelles vont être les grandes étapes ?
- Collecter les informations (échantillon)
- Caractériser l'observation
- Définir la population, l’échantillon
- Définir la Variable Aléatoire d’étude
- Poser une Hypothèse nulle (notée
 ) et son hypothèse alternative H1 ) et son hypothèse alternative H1
- Fixer un risque seuil
 arbitraire (généralement 5%, risque standard) arbitraire (généralement 5%, risque standard)
- Calculer
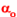 , probabilité d'observer sous , probabilité d'observer sous  un tel évènement ou des évènements encore moins probables (et calculer éventuellement un tel évènement ou des évènements encore moins probables (et calculer éventuellement 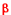 ) en utilisant les tables des lois de distribution connues : Binomiale, Poisson, Normale, Chi-Deux, Student, Fisher ... ) en utilisant les tables des lois de distribution connues : Binomiale, Poisson, Normale, Chi-Deux, Student, Fisher ...
- Conclure en comparant notamment
 et et 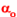 . .
Cahier des charges de la résolution d'un test d'hypothèse
Exemple introductif : "Le médicament miracle"
Un laboratoire pharmaceutique garantit que son médicament destiné au traitement d'une affection cutanée est efficace dans 80 % des cas. Un groupe indépendant a collecté les données de cabinets médicaux d'une région où 40 patients atteints par l'affection ont été traités par le médicament. Parmi eux, 28 ont été définitivement guéris. Pour les 12 autres patients le médicament a été sans effet, ils ont dû changer de traitement.
- Ces résultats sont-ils conformes à l'affirmation du laboratoire pharmaceutique ?
- En se basant sur les chiffres du laboratoire pharmaceutique, quelle est la probabilité de trouver entre 75% et 85 % de malades guéris par le médicament dans un tel échantillon ?
- Au risque seuil de 5%, donner les limites de la valeur attendue pour 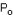 . .
- Quelle seraient ces limites si l'on avait étudié un échantillon de 150 personnes traitées par le médicament dont 105 auraient été guéries par le médicament ?
"Le médicament miracle" - Construction de l'hypothèse
Population : l'ensemble des malades atteints de l'affection cutanée et traitées par le médicament.
Echantillon : 40 patients (issus de cabinets médicaux de la région) atteints par l'affection traités par le médicament.
V.A. d'étude : 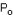 = "pourcentage de personnes guéries par le médicament dans un échantillon de 40 personnes" = "pourcentage de personnes guéries par le médicament dans un échantillon de 40 personnes"
Observation : 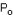 = 28/40 = 70% guéris = 28/40 = 70% guéris
Ho : l'échantillon provient d'un population définie par un taux de guérison par le médicament de  =0,8. =0,8.
Les différences entre ce paramètre et la valeur observée dans l'échantillon sont imputables au hasard des fluctuations d'échantillonnage.
Seuil : fixons un seuil 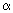 =5% à ne pas dépasser. =5% à ne pas dépasser.
Méthode (cahier des charges d'un test d'hypothèses)
- Définir l'échantillon et caractériser l'observation (collecter les données, tri à plat).
- Définir la variable aléatoire.
- Définir la population (que connaît-on de cette population ? Loi de distribution suivie par la variable aléatoire d'étude dans la population ?).
- Poser une Hypothèse nulle (notée
 ) permettant de raccorder l'observation faite sur un échantillon à une population donnée. ) permettant de raccorder l'observation faite sur un échantillon à une population donnée.
- Le test va alors consister à évaluer la probabilité d'obtenir, par hasard sous l'hypothèse nulle, l'observation dont on dispose (ainsi que les évènements encore moins probables).
Il faut se fixer un risque seuil  arbitraire (généralement 5%) que l'on ne doit pas dépasser pour accepter l'hypothèse nulle. Ce seuil sera comparé à la probabilité arbitraire (généralement 5%) que l'on ne doit pas dépasser pour accepter l'hypothèse nulle. Ce seuil sera comparé à la probabilité 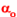 d'obtenir par le hasard sous d'obtenir par le hasard sous  les observations dont on dispose. les observations dont on dispose.
- La conclusion du test dépendra du résultat de cette comparaison.
Si  > > 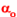 on rejette l'hypothèse nulle avec un risque de première espèce on rejette l'hypothèse nulle avec un risque de première espèce 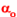 de se tromper en la rejetant alors qu'elle est vraie. de se tromper en la rejetant alors qu'elle est vraie.
Si  ≥ ≥ 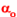 l'hypothèse nulle est acceptable (acceptable jusqu'au seuil l'hypothèse nulle est acceptable (acceptable jusqu'au seuil 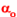 ) )
Dans certains cas nous pourrons définir un risque de seconde espèce, noté 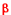 , probabilité d'erreur d'admettre que , probabilité d'erreur d'admettre que  , qui est fausse, puisse être acceptable alors que c'est une hypothèse alternative , qui est fausse, puisse être acceptable alors que c'est une hypothèse alternative  qui est vraie. qui est vraie.
- L'expérimentateur peut alors prendre une décision en fonction du résultat du test (+bon sens ...)
Test de conformité à une proportion exacte
Il s'agit de confronter une valeur de la variable aléatoire 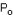 , observée dans un échantillon, à la valeur exacte du paramètre , observée dans un échantillon, à la valeur exacte du paramètre  , dans la population. , dans la population.
Tout revient à déterminer si la différence observée entre les 2 valeurs est significative ou si elle peut s'expliquer par le hasard des fluctuations d'échantillonnage.
Le critère de test utilisé est
|
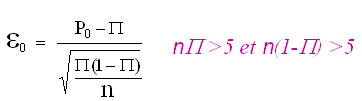 |
avec
|
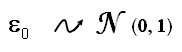 |
"Le médicament miracle" - Construction du test d'hypothèse
Population : l'ensemble des malades atteints de l'affection cutanée.
Echantillon : 40 patients (issus de cabinets médicaux de la région) atteints par l'affection traités par le médicament
V.A. d'étude :  = "pourcentage de personnes guéries par le médicament dans un échantillon de 40 personnes". = "pourcentage de personnes guéries par le médicament dans un échantillon de 40 personnes".
Observation :  =28/40 = 70% guéris. =28/40 = 70% guéris.
Ho : l'échantillon provient d'une population définie par un taux de guérison par le médicament de  =0,8. =0,8.
Les différences entre ce paramètre et la valeur observée dans l'échantillon sont imputables au hasard des fluctuations d'échantillonnage.
Seuil : fixons un seuil  =5% à ne pas dépasser. =5% à ne pas dépasser.
Calcul de  o : sous Ho, o : sous Ho, 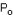 subit des fluctuations d'échantillonnage de nature binomiale subit des fluctuations d'échantillonnage de nature binomiale 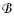 (40, 0,8) approximables par une distribution normale (0,8x40 et 0,2x40 tous deux supérieurs à 5) de moyenne (40, 0,8) approximables par une distribution normale (0,8x40 et 0,2x40 tous deux supérieurs à 5) de moyenne 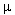 = =  = 0,8 et d'écart-type = 0,8 et d'écart-type 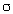 = (0,8x0,2/40) = (0,8x0,2/40)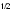 = 0,063 ; = 0,063 ;  (0,8, 0,063) (0,8, 0,063)
Test bilatéral : à priori, il y a autant de chances que le hasard induise des différences négatives que positives.
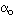 =P((Po<0,7) ou (Po>0,9)) = 2xP(Po>0,9), probabilité d'observer un tel échantillon sous Ho. =P((Po<0,7) ou (Po>0,9)) = 2xP(Po>0,9), probabilité d'observer un tel échantillon sous Ho.
Z=(Po-0,8)/0,063 est normale centrée réduite N(0,1)
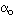 =2xP(Z>(0,9-0,8)/0,063) =2xP(Z>(0,9-0,8)/0,063)
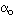 o=2xP(Z>1,58) o=2xP(Z>1,58)
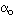 o=2×0,057053=0,114 (lecture table o=2×0,057053=0,114 (lecture table 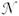 (0,1)) (0,1))
Conclusion : 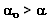 ; Ho est acceptable au risque seuil ; Ho est acceptable au risque seuil  =5% =5%
De telles différentes peuvent s'expliquer par le hasard des fluctuations d'échantillonnage.
Ces résultats sont conformes à l'affirmation du laboratoire pharmaceutique.
Remarques : Aucune certitude mais la Statistique peut expliquer ces différences.
Une étude sur d'autres échantillons serait intéressante.
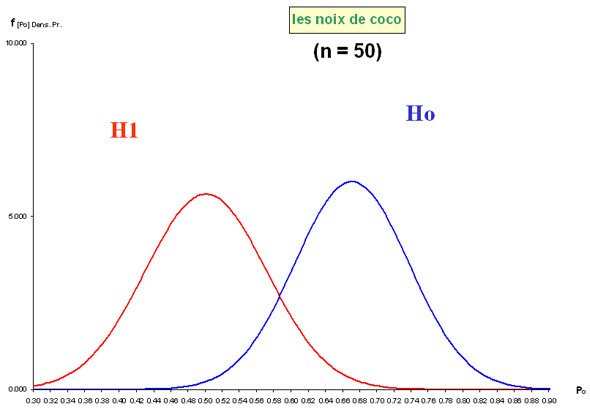
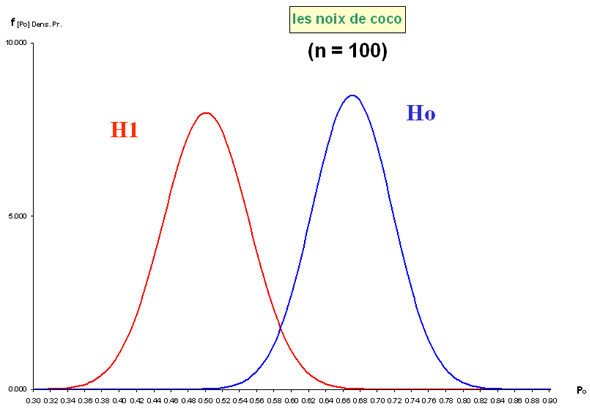
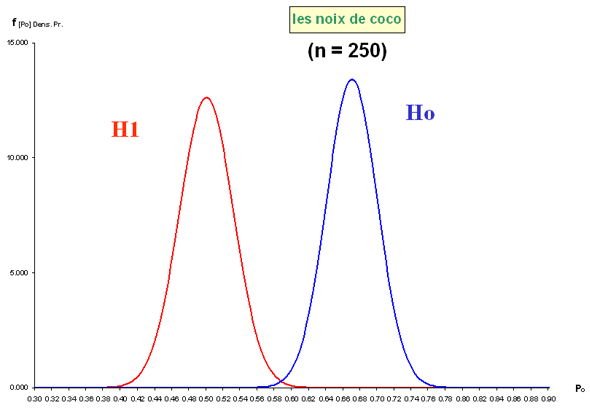
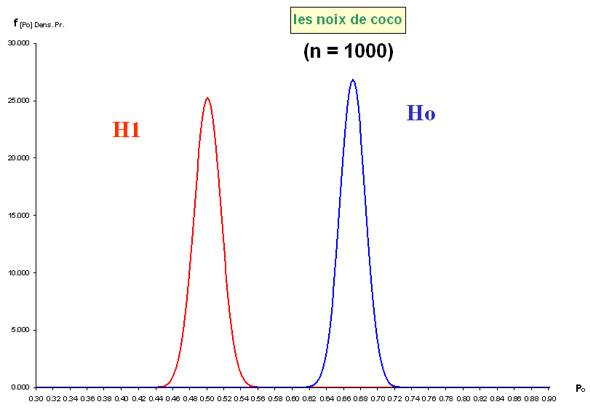
Exercice : "Les noix de coco"
Un producteur déclare à son client que deux tiers des noix de coco qu’il lui fournit sont de tailles supérieures à une certaine limite qu'ils ont fixée ensemble. Le distributeur conteste cette statistique et avance que d'après les ventes qu'il a réalisées, ce sont seulement la moitié des noix de coco qui sont de taille suffisante (atteignant ou dépassant la limite fixée).
Pour en avoir le coeur net, un échantillon de 50 noix de coco est prélevé au hasard de la production destinée au client. Le résultat tombe bientôt : 30 noix de l'échantillon sont de taille supérieure à la limite fixée.
Que peut-on en conclure ?
| Les noix de coco |
|
|
|
|
|
|
| test unilatéral |
|
|
|
|
|
|
seuil 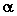 |
0,05 |
|
|
|
|
|
| Po |
0,6 |
|
|
|
|
|
| 1ère solution |
|
|
|
|
|
|
| II sous Ho |
0,067 |
|
|
|
|
|
| II sous H1 |
0,5 |
|
|
|
|
|
| N |
25 |
50 |
100 |
150 |
250 |
1000 |
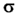 (Ho) (Ho) |
0,094 |
0,067 |
0,047 |
0,038 |
0,030 |
0,015 |
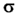 (H1) (H1) |
0,100 |
0,071 |
0,050 |
0,041 |
0,032 |
0,016 |
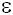 o, critère de test sous Ho o, critère de test sous Ho |
0,707 |
1,000 |
1,414 |
1,732 |
2,236 |
4,472 |
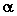 0 = P(Po<0,6) 0 = P(Po<0,6) |
24,0% |
15,9% |
7,9% |
4,2% |
1,3% |
0,0% |
position limite pour 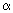 = 5% = 5% |
0,51 |
0,56 |
0,59 |
0,60 |
0,62 |
0,64 |
| critère de test sous H1 |
0,120 |
0,811 |
1,787 |
2,536 |
3,724 |
8,995 |
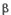 = P(Po<limite) = P(Po<limite) |
45,2% |
20,9% |
3,7% |
0,6% |
0,0% |
0,0% |
conclusion |
Ho acceptable |
Ho acceptable |
Ho acceptable |
différences
significatives |
différences
significatives |
différences
significatives |
| 2ème solution |
|
|
|
|
|
|
| II sous Ho |
0,5 |
|
|
|
|
|
| II sous H1 |
0,067 |
|
|
|
|
|
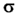 (Ho) (Ho) |
0,100 |
0,071 |
0,050 |
0,041 |
0,032 |
0,0158 |
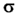 (H1) (H1) |
0,094 |
0,067 |
0,047 |
0,038 |
0,030 |
0,015 |
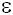 o, critère de test sous Ho o, critère de test sous Ho |
1,000 |
1,414 |
2,000 |
2,449 |
3,162 |
6,325 |
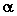 0 = P(Po<0,6) 0 = P(Po<0,6) |
15,9% |
7,9% |
2,3% |
0,7% |
0,1% |
0,0% |
position limite pour 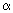 = 5% = 5% |
0,66 |
0,62 |
0,58 |
0,57 |
0,55 |
0,53 |
| critère de test sous H1 |
0,028 |
0,761 |
1,796 |
2,591 |
3,851 |
9,441 |
 = P(Po<limite) = P(Po<limite) |
48,9% |
22,3% |
3,6% |
0,5% |
0,0% |
0,0% |
conclusion |
Ho acceptable |
Ho acceptable |
Ho acceptable |
différences
significatives |
différences
significatives |
différences
significatives |
Une première approche intuitive de la notion de maximum de vraisemblance peut-être évoquée dans le cadre des tests d’hypothèses. Elle consiste a considérer et tester plusieurs hypothèses nulles pour sélectionner, comme la plus vraisemblable, celle associée au plus fort degré de signification  o. o.
Dans l’exemple des "noix de coco",
il apparaît que (Ho :  = 2/3) est l’hypothèse nulle la plus vraisemblable. = 2/3) est l’hypothèse nulle la plus vraisemblable.
Risque de seconde espèce
 = probabilité d'accepter à tort Ho = probabilité d'accepter à tort Ho
C'est-à-dire probabilité :
- d'acepter
 alors que c'est l'hypothèse alternative alors que c'est l'hypothèse alternative 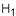 qui est vraie qui est vraie
- de réalisation de la V.A. sous l'hypothèse 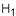 dans le domaine d'acceptation de dans le domaine d'acceptation de 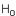
Puissance du test
1 - 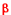 = puissance du test = puissance du test
-probabilité de mettre en évidence que l'hypothèse nulle 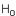 est fausse lorsqu'elle est effectivement fausse (voir schéma) est fausse lorsqu'elle est effectivement fausse (voir schéma)
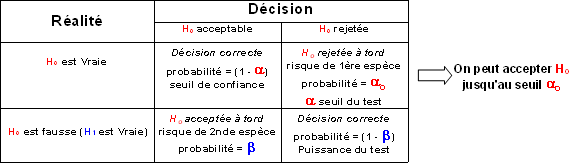
Les quatre résultats possibles d'un test d'hypothèses
La réduction de  entraîne l'accroissement de entraîne l'accroissement de 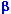 ! !
L'hypothèse nulle 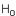 permet de calculer des probabilités. permet de calculer des probabilités.
Ho est acceptable tant que l'on n'a pas acquis la quasi-certitude qu'elle est fausse.
Si l'on peut démontrer que l'observation est improbable sous 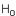 celle-ci est rejetée, au profit de l'hypothèse alternative celle-ci est rejetée, au profit de l'hypothèse alternative 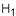 . Sinon . Sinon 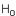 est acceptable (on ne conclue pas). est acceptable (on ne conclue pas).
En pratique, on divise la distribution en :
 Domaine d'acceptation de Domaine d'acceptation de  au seuil au seuil  , région pour laquelle la V.A. d'étude peut prendre des valeurs, avec une probabilité 1- , région pour laquelle la V.A. d'étude peut prendre des valeurs, avec une probabilité 1-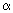 , si , si 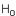 est vraie. est vraie.
 Domaine de rejet de Domaine de rejet de 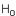 au seuil au seuil 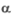 , région pour laquelle la V.A. d'étude prend des valeurs improbables (petite probabilité , région pour laquelle la V.A. d'étude prend des valeurs improbables (petite probabilité 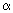 ) si ) si 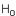 est vraie. est vraie.
Le seuil de rejet, limite entre ces deux régions, est la valeur (liée à 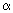 ), à partir de laquelle l'expérimentateur décide de rejeter ), à partir de laquelle l'expérimentateur décide de rejeter 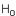 en faveur de en faveur de 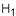 . .
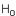 est acceptable tant que l'observation ne dépasse pas cette valeur seuil. est acceptable tant que l'observation ne dépasse pas cette valeur seuil.
Le seuil de rejet est calculable par rapport à la distribution modèle considérée.
 mesure le risque que l'expérimentateur accepte de prendre en rejetant à tort mesure le risque que l'expérimentateur accepte de prendre en rejetant à tort 
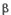 mesure le risque que l'expérimentateur accepte de prendre en acceptant à tort mesure le risque que l'expérimentateur accepte de prendre en acceptant à tort 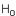
La valeur observée dans l'échantillon 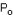 est comparée au seuil de rejet est comparée au seuil de rejet 
Si 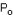 appartient au domaine d'acceptation de appartient au domaine d'acceptation de 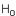 , on préfère rejeter , on préfère rejeter 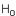 , trop peu vraisemblable, en faveur de , trop peu vraisemblable, en faveur de 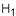 > l'observation nous semble suffisamment extraordinaire pour nous permettre de rejeter > l'observation nous semble suffisamment extraordinaire pour nous permettre de rejeter 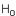 avec une faible probabilité de se tromper. avec une faible probabilité de se tromper.
L'inférence et la déduction statistique aident l'expérimentateur à prendre une décision en considérant le risque d'erreur associé (1ère et 2ème espèce)
Autre préoccupation :
Test d'homogénéité concernant deux valeurs de proportions observées dans deux échantillons (tirés au hasard).
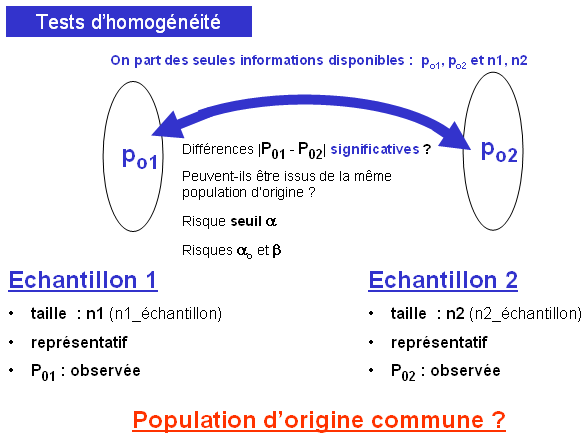
Test d'homogénéité de deux proportions observées
Il s'agit de confronter 2 valeurs de la variable aléatoire 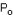 , , 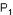 et et 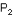 , observées dans deux échantillons (supposés provenir d'une population commune sous l'hypothèse nulle). Tout revient à déterminer si la différence observée entre les deux valeurs est significative ou peut, au contraire, s'expliquer par le hasard des fluctuations d'échantillonnage. , observées dans deux échantillons (supposés provenir d'une population commune sous l'hypothèse nulle). Tout revient à déterminer si la différence observée entre les deux valeurs est significative ou peut, au contraire, s'expliquer par le hasard des fluctuations d'échantillonnage.
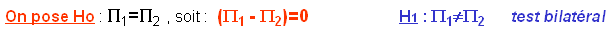
 Egalité des deux paramètres exacts dans les deux populations d'origine ; les différences observées dans les échantillons étant dues au hasard des fluctuations d'échantillonnage. Egalité des deux paramètres exacts dans les deux populations d'origine ; les différences observées dans les échantillons étant dues au hasard des fluctuations d'échantillonnage.
 On est ainsi ramené à comparer la différence ( On est ainsi ramené à comparer la différence (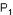 - - 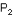 ) à la valeur exacte 0. ) à la valeur exacte 0.
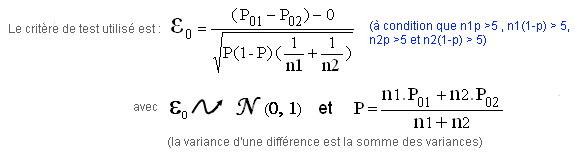
Le premier jugement que l’on tire d’un test qui permet de conclure est un jugement de signification (les différences sont significatives).
Le jugement d’interprétation permet, quant à lui, de déterminer si c’est la présence ou l’absence d’un caractère est à l’origine de ces différences. Pour discuter de la causalité à l’issue d’un test, il faut s’assurer du contrôle d’un des deux caractères étudiés.
Démarche / situation expérimentale
Lorsque l’expérience se conduit avec un facteur contrôlé (par l’expérimentateur).
Au cours de la constitution de l’échantillon, on reste libre d’un caractère (exemple : individu i traité ou non). On ne peut affirmer la causalité hors d’une démarche expérimentale qui est la seule qui permet d’assurer que les individus constituant l’échantillon sont comparables ou homogènes sauf pour ce qui concerne le caractère contrôlé (attribué par tirage au sort).
Démarche / situation d'observation
Lorsque l’expérience se conduit sur la base de deux facteurs aléatoires (non contrôlés par l’expérimentateur ; ex : surpoids et maladie rare, couleur des yeux et couleur cheveux, effets secondaires)
 Il faudra faire des recherches (par ex sur les gènes) pour conclure plus finement. Il faudra faire des recherches (par ex sur les gènes) pour conclure plus finement.
Exemple typique : comparaison de deux traitements (un des traitement est la référence, constitution d’un groupe témoin recevant le traitement de référence) ou mise en évidence de l’effet d’un traitement (constitution d’un groupe témoin recevant un placebo. Procédure « d’aveugle » où les malades ne doivent pas savoir s’ils reçoivent le traitement ou le placebo. Procédure de « double aveugle » si l’attribution du traitement ou du placebo se fait en plus à l’insu du médecin).
Exercice : "Traitement contre la grippe" (un grand classique !)
On veut comparer deux formes de traitement T1 et T2 contre la grippe. Dans ce but, on décide d'attribuer T1 ou T2 par tirage au sort aux 300 personnes qui se présentent à un service hospitalier. Après 5 jours de traitement, on constate que sur les 200 personnes qui ont suivi T1, 175 sont guéries et sur les 100 autres qui ont suivi T2, 70 sont guéries.
A - Pensez-vous que la nature du traitement influe sur le taux de guérison en 5 jours ?
B - Dans chacun des 2 groupes ; on a noté le sexe de chaque individu.
Les proportions de femmes observées sont les suivantes : 52 % dans le groupe T1 et 49 % dans le groupe T2. Au risque d'erreur 5%, la différence entre les 2 pourcentages observés est-elle significative ?
Ce résultat pouvait-il être attendu ?
C - Sachant que sur les 104 femmes ayant suivi le traitement T1, 90 sont guéries et que sur les 49 femmes ayant suivi le traitement T2, 40 sont guéries, pensez-vous que la guérison soit liée au sexe, quel que soit le traitement suivi ?
A - 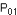 = 175/200 = 0,875 ; = 175/200 = 0,875 ; 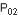 = 70/100 = 0,700 ; = 70/100 = 0,700 ;
P = (200x0,875+100x7)/(200+100) = 0,817
(la plus petite quantité à comparer à 5 étant 0.183x100=18.3 est bien > 5, on peut appliquer l’approximation normale des fluctuations d’échantillonnage)
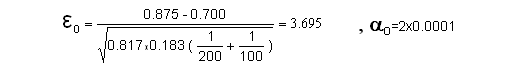
Conclusion : si l'on pose 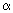 =5% et même =5% et même 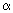 =1% > =1% >  rejetée ; rejetée ;
au seuil de 1% on peut dire, pratiquement sans aucun risque de se tromper (en rejetant 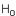 ), que la nature du traitement influe sur le taux de guérison (jugement d'interprétation) ; les différences étant significatives (jugement de signification) jusqu'au seuil ), que la nature du traitement influe sur le taux de guérison (jugement d'interprétation) ; les différences étant significatives (jugement de signification) jusqu'au seuil 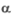 =0,02% (auquel on peut encore rejeter de =0,02% (auquel on peut encore rejeter de 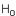 ). ).
Situation expérimentale
B - 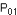 = 0,52 ; = 0,52 ; 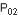 = 0,49 ; P=0,51 (la plus petite quantité à comparer à 5 étant 0.49x100=49 est bien > 5) = 0,49 ; P=0,51 (la plus petite quantité à comparer à 5 étant 0.49x100=49 est bien > 5)
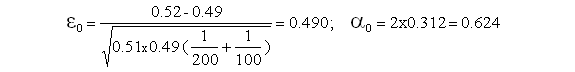
décision : 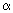 =5% > =5% >  acceptable ; (jusqu'à acceptable ; (jusqu'à 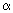 =62.4% !) =62.4% !)
La différence entre les 2 pourcentages n'est pas significative au seuil de 5%
C - Quelque soit le traitement suivi > on regroupe les données des deux traitements T1 et T2. Les deux échantillons considérés sont les hommes et les femmes sélectionnéspour être traités (indifféremment par T1 ou T2).
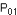 = 130/153 = 0,850 (90+40)=130 femmes guéries sur (104+49)=153 femmes au total = 130/153 = 0,850 (90+40)=130 femmes guéries sur (104+49)=153 femmes au total
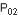 = 115/147 = 0,782 (175+70)-(90+40)=115 hommes guéris sur (300-104+49)=147 hommes = 115/147 = 0,782 (175+70)-(90+40)=115 hommes guéris sur (300-104+49)=147 hommes
P = 0,817, 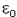 = 1,52 ; = 1,52 ; 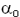 = 0.064x2 = 0.128 (la table de la loi normale centrée réduite donne = 0.064x2 = 0.128 (la table de la loi normale centrée réduite donne 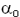 /2) /2)
(la plus petite quantité à comparer à 5 étant 0.183x100 = 18.3 est bien > 5)
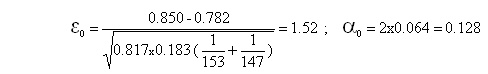
décision :  =5% > =5% >  acceptable ; (jusqu'à acceptable ; (jusqu'à  =12.8% !) =12.8% !)
Au seuil de 5 %, les différences ne sont pas assez significatives pour que l’on puisse dire que le taux de guérison soit lié au sexe quelque soit le traitement suivi.
4. Fluctuations d’échantillonnage d’une moyenne observée
Plusieurs cas possibles …
- La variable étudiée dans la population ou l’échantillon est X
- La variable d’échantillonnage est sa moyenne 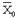
- Loi suivie par 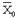 : il sera nécessaire de vérifier que : il sera nécessaire de vérifier que 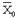 (le cas échéant X) est distribuée normalement. (le cas échéant X) est distribuée normalement.
- Connaissance de σ (population) ?
- Théorème « central limit »
Dans tous les tests sur la moyenne, il est souvent utile de démontrer que 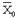 suit une loi normale suit une loi normale
Théorème « central limit »
Pour appliquer le théorème de la limite centrale il faut que σ soit connu!
Si X, variable aléatoire d'étude, est distribuée de façon quelconque dans une population de moyenne µ et écart type σ, paramètres exacts connus,
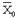 , moyenne observée dans un échantillon de taille n, prélevé dans cette population tend vers une distribution normale de même moyenne µ et d’écart-type , moyenne observée dans un échantillon de taille n, prélevé dans cette population tend vers une distribution normale de même moyenne µ et d’écart-type 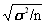 . .
 Lorsque la loi de distribution suivie par la variable d'étude X est normale dans la population, Lorsque la loi de distribution suivie par la variable d'étude X est normale dans la population, 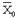 est réellement distribuée normalement est réellement distribuée normalement
 Lorsque la loi de distribution suivie par la variable d'étude X n'est pas connue dans la population, on peut considérer que Lorsque la loi de distribution suivie par la variable d'étude X n'est pas connue dans la population, on peut considérer que 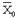 est distribuée normalement, dès que n ≥ 30 est distribuée normalement, dès que n ≥ 30
Si n < 30 : il est parfois possible d'émettre l'hypothèse que la variable d'étude X est supposée distribuée normalement dans la population (souvent le cas en biologie) ou au moins que la distribution est symétrique. Dans le cas contraire, on ne pourra pas traiter le problème en utilisant la loi normale.
Cas où σ, écart type de la population, est connu
Intervalle de pari,
au risque, encadrant les valeurs de 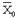 observables dans un échantillon tiré au hasard d’une population caractérisée par le paramètre exact µ (caractéristique) : observables dans un échantillon tiré au hasard d’une population caractérisée par le paramètre exact µ (caractéristique) :
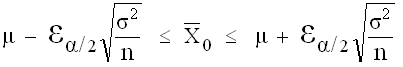
La probabilité de trouver 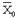 dans cet intervalle est (1-α) dans cet intervalle est (1-α)
Seuil standard : α = 5%
Exemple introductif "Simulation d'échantillonnage"
Une expérience d'échantillonnage consiste à simuler le prélèvement de 100 échantillons de 20 individus dans une population de sujets âgés de moins de 30 ans.
Chez ces sujets, le taux d’une enzyme y est supposée distribuée normalement
avec une moyenne exacte µ = 1 mg/ml et un écart-type σ = 0,3 mg/ml.
1) Quel est l'intervalle de pari sur 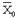 au risque α = 1% ? au risque α = 1% ?
2) Sur les 100 valeurs observées, combien de valeurs observées de la moyenne vous attendez-vous à trouver dans cet intervalle ?
3) Donnez l'intervalle de pari de la variable centrée et réduite au risque α = 1%.
4) Sur les 100 ICa construits au risque α, combien en moyenne recouvrent la valeur exacte µ = 1 mg/ml ?
Intervalle de pari de la variable d’échantillonage 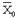 Cas où σ, écart type de la population, n’est pas connu Cas où σ, écart type de la population, n’est pas connu
Intervalle de pari,
au risque α, encadrant les valeurs de 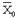 observables dans un échantillon tiré au hasard d’une population caractérisée par le paramètre exact µ (caractéristique) : observables dans un échantillon tiré au hasard d’une population caractérisée par le paramètre exact µ (caractéristique) :
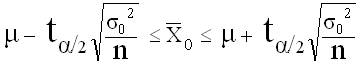
La probabilité de trouver 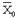 dans cet intervalle est (1-α) dans cet intervalle est (1-α)
[seuil standard : α = 5 %]
On se sert des tables de la loi de Student à n-1 ddl
Condition d’application : Il faut que la V.A. d’étude X suive une loi normale dans la population
Cas où σ, écart type de la population, est connu
Situation rare car lorsque µ est inconnue, σ est généralement inconnu lui aussi !
Intervalle de confiance , au risque a , encadrant les valeurs attendues pour le paramètre exact µ (caractéristique), à partir de la connaissance 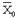 de observée dans un échantillon supposé représentatif : de observée dans un échantillon supposé représentatif :
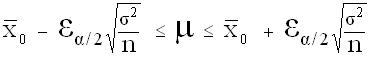
La probabilité de trouver µ dans cet intervalle est (1-α)
Seuil standard : α = 5 %
On définit ainsi plusieurs populations pouvant rendre compte de l'échantillon observé.
Cas où σ, écart-type de la population, est inconnu
Intervalle de confiance , au risque a , encadrant les valeurs attendues pour le paramètre exact µ (caractéristique) , à partir de la connaissance de 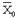 observée dans un échantillon supposé représentatif : observée dans un échantillon supposé représentatif :
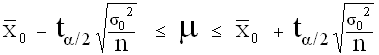
La probabilité de trouver µ dans cet intervalle est (1-α)
Seuil standard : α = 5%
On définit ainsi plusieurs populations pouvant rendre compte de l'échantillon observé.
Test de conformité à une moyenne exacte µ dans le cas où σ, écart type de la population est connu
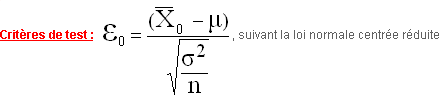
Même raisonnement que pour l’étude des fluctuations d’échantillonnage d’une proportion observé
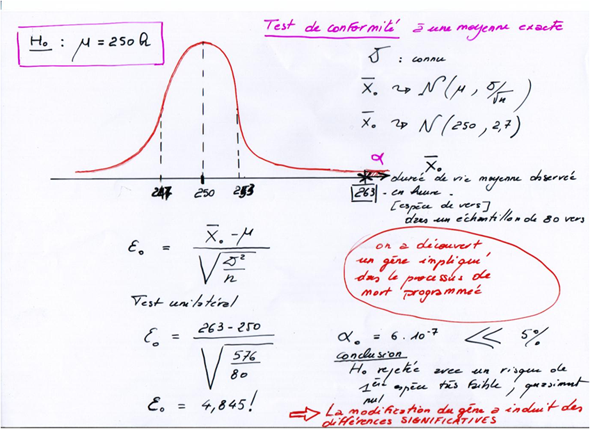
Exemple introductif "Vers une vie éternelle"
Un laboratoire de recherche étudie, sur une nouvelle espèce de vers (C. marginalus), les gènes pouvant être impliqués dans la mort programmée. Chez ces vers, la durée de vie est caractérisée par une moyenne exacte µ = 250 heures et un écart-type exact σ = 24 heures.
Après modification d'un gène, supposé intervenir dans la mort programmée, on a relevé dans un échantillon de 80 vers une durée de vie moyenne de 263 heures et un écart type de 27 heures.
Que peut-on en conclure?
Situation d’expérience
L’écart-type de l’échantillon n’est pas une donnée utilisée
Test de conformité à une moyenne exacte µ, Cas où σ, écart type de la population, n’est pas connu
Dans ce cas, on se base sur la seule connaissance de 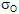 (calculé à partir des données de l'échantillon). Contrairement à (calculé à partir des données de l'échantillon). Contrairement à 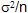 , , 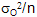 n'est plus une constante mais une variable aléatoire suivant une loi de distribution de Student. Le critère de test utilisé sera n'est plus une constante mais une variable aléatoire suivant une loi de distribution de Student. Le critère de test utilisé sera 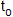 , à (n-1) degré de liberté. On se servira de la table échantillonnée de Student pour trouver les valeurs de la probabilité , à (n-1) degré de liberté. On se servira de la table échantillonnée de Student pour trouver les valeurs de la probabilité 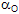 connaissant connaissant 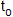 ou celles de ou celles de 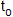 connaissant connaissant 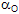 . La distribution de Student est symétrique ; elle pourra dans la pratique être approchée, avec peu d'erreur, par une distribution normale lorsque n est suffisamment grand ( n> 30, théorème central limite ). . La distribution de Student est symétrique ; elle pourra dans la pratique être approchée, avec peu d'erreur, par une distribution normale lorsque n est suffisamment grand ( n> 30, théorème central limite ).
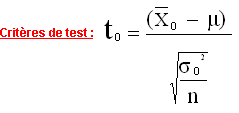
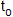 suivant une loi de Student à n-1 degrés de libertés (ddl) suivant une loi de Student à n-1 degrés de libertés (ddl)
Condition d’application : Il faut que la V.A. d’étude X suive une loi normale dans la population
Exemple introductif "Vers une vie éternelle"
Un laboratoire de recherche étudie, sur une nouvelle espèce de vers (C. marginalus), les gènes pouvant être impliqués dans la mort programmée. Chez ces vers, la durée de vie est caractérisée par une moyenne exacte µ = 250 heures.
Après modification d'un gène, supposé intervenir dans la mort programmée, on a relevé dans un échantillon de 80 vers une durée de vie moyenne de 263 heures et un écart type de 27 heures.
- Que peut-on en conclure?
- Même question si l’observation avait été faite sur un échantillon de 25 vers ?
Situation d’expérience
L’écart-type de l’échantillon est utilisé en absence de la connaissance de σ (population) => test t
5. Comparaison de 2 variances observées / de 2 moyennes observées
Tests d’homogénéité
Test de comparaison de 2 variances observées
Hypothèse nulle 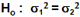
 population commune / différences dues au hasard population commune / différences dues au hasard
On se servira de la table échantillonnée de Fisher pour trouver les valeurs de la probabilité  connaissant F ou celles de F connaissant connaissant F ou celles de F connaissant 
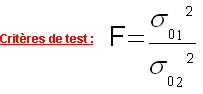
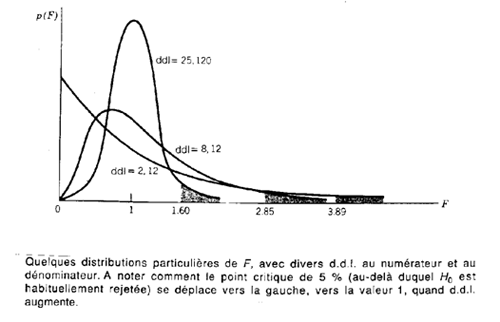
F suivant une loi de Fisher à 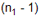 et et 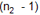 degrés de libertés (ddl) degrés de libertés (ddl)
Test F
Pour mesurer la crédibilité de Ho, on calcule sa probabilité critique (probabilité de la queue de distribution de F située au delà de la valeur observée).
Lecture de la table de Fisher dépendant des degrés de libertés de la variance du numérateur 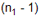 et de ceux de la variance du dénominateur et de ceux de la variance du dénominateur 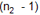

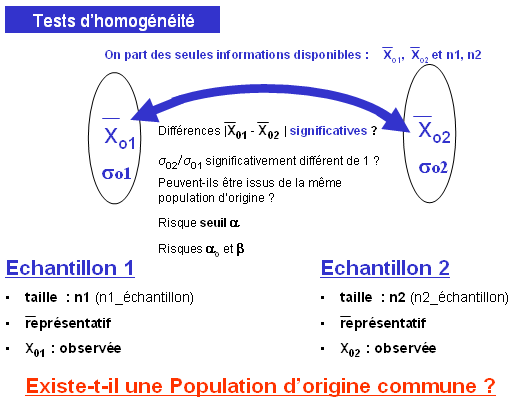
Test d’homogénéité de 2 moyennes observées

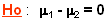
 population d’origine commune / différences dues au hasard population d’origine commune / différences dues au hasard
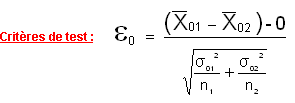
On se sert de la table échantillonnée de la loi de student pour trouver les valeurs de la probabilité 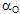 connaissant connaissant 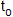 ou celles de ou celles de 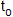 connaissant connaissant 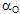 . .

 Test F préalable sur les variances observées pour pouvoir calculer la variance commune si elle existe ( Test F préalable sur les variances observées pour pouvoir calculer la variance commune si elle existe ( , hypothèse d’égalité des variances des 2 populations, acceptable)
L’approximation de la variance supposée commune des variables étudiées est alors : , hypothèse d’égalité des variances des 2 populations, acceptable)
L’approximation de la variance supposée commune des variables étudiées est alors :
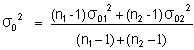
Si le test F échoue, on ne peut pas conclure à l’égalité des 2 moyennes car le test t ne peut être réalisé !
Test d’homogénéité de 2 moyennes observées

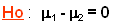
 population d’origine commune / différences dues au hasard population d’origine commune / différences dues au hasard
On se servira de la table échantillonnée de la loi normale centrée réduite pour trouver les valeurs de la probabilité 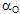 connaissant connaissant 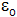 ou celles de ou celles de 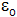 connaissant connaissant 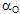 . .
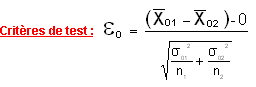
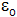 suivant la loi N (0,1) suivant la loi N (0,1)
Exercice "Une production machine-dépendante ?"
On veut comparer la production de deux machines artisanales. Le volume de parfum déposé par ces machines dans des flacons destinés à la vente a été mesuré en ml. Les statistiques figurent ci-dessous. Le laborantin qui en est responsable soupçonne une production dépendante de la machine.
Machine 1 |
Machine 2 |
47 |
54 |
53 |
50 |
49 |
51 |
50 |
51 |
46 |
49 |
Qu’en pensez-vous?
 Attention, il s’agit de petits échantillons : Attention, il s’agit de petits échantillons :
les tailles des 2 échantillons sont inférieures à 30.
 Test F préalable comparant les variances observées Test F préalable comparant les variances observées

si les variances sont les mêmes (même population d’origine),
le rapport des deux variances observées doit tendre vers 1.
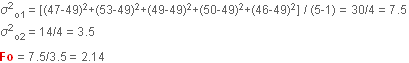
Cette valeur est plus petite que 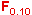 (4.11) lue sur la table de Fisher à 4 ddl au numérateur (intervenant dans le calcul de la première variance)
et 4 ddl au dénominateur (intervenant dans le calcul de la deuxième variance).
Ho est donc largement acceptable (jusqu’au risque seuil de 10 % et même presque 25 %)
et l’on peut calculer une variance commune : (4.11) lue sur la table de Fisher à 4 ddl au numérateur (intervenant dans le calcul de la première variance)
et 4 ddl au dénominateur (intervenant dans le calcul de la deuxième variance).
Ho est donc largement acceptable (jusqu’au risque seuil de 10 % et même presque 25 %)
et l’on peut calculer une variance commune :
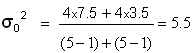
Le test sur les variance étant positif, on peut poursuivre le test sur les moyennes
Test t sur les deux moyennes observées
(on supposera que la production est distribuée normalement dans les 2 populations)

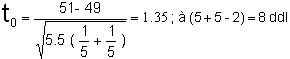
(la variance commune calculée est injectée dans le calcul de 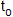 ) )
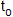 < 1.86 ( à 8 ddl)
(test bilatéral, il y autant de chance d’observer des écarts positifs que des écarts négatifs) < 1.86 ( à 8 ddl)
(test bilatéral, il y autant de chance d’observer des écarts positifs que des écarts négatifs) 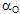 > 10% > 10%
Ho est acceptable, au moins jusqu’au seuil de 10%, et même 20 % (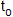 pour 20% est 1.39)
les différences sont imputables au hasard des fluctuations d’échantillonnage. On ne peut affirmer sans risque de se tromper que la production est machine dépendante. pour 20% est 1.39)
les différences sont imputables au hasard des fluctuations d’échantillonnage. On ne peut affirmer sans risque de se tromper que la production est machine dépendante.
On veut comparer maintenant la production de la première machine avec celle d’une autre machine. Les statistiques figurent ci-dessous. Le laborantin soupçonne toujours une production dépendante de la machine.
Machine 1 |
Machine 3 |
47 |
55 |
53 |
54 |
49 |
58 |
50 |
61 |
46 |
52 |
Qu’en pensez-vous?
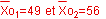 Attention, il s’agit de petits échantillons : Attention, il s’agit de petits échantillons :
les tailles des 2 échantillons sont inférieures à 30.
 Test F préalable comparant les variances observées Test F préalable comparant les variances observées
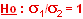 si les variances sont les mêmes (même population d’origine),
le rapport des deux variances observées doit tendre vers 1. si les variances sont les mêmes (même population d’origine),
le rapport des deux variances observées doit tendre vers 1.
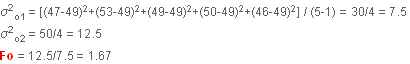
Cette valeur est plus petite que  (2.06) lue sur la table de Fisher à 4 ddl au numérateur (intervenant dans le calcul de la première variance)
et 4 ddl au dénominateur (intervenant dans le calcul de la deuxième variance).
Ho est donc largement acceptable (jusqu’au risque seuil de 25 %)
et l’on peut calculer une variance commune : (2.06) lue sur la table de Fisher à 4 ddl au numérateur (intervenant dans le calcul de la première variance)
et 4 ddl au dénominateur (intervenant dans le calcul de la deuxième variance).
Ho est donc largement acceptable (jusqu’au risque seuil de 25 %)
et l’on peut calculer une variance commune :
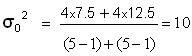
Test t sur les deux moyennes observées
(on supposera que la production est distribuée normalement dans les 2 populations)

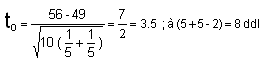
(la variance commune calculée est injectée dans le calcul de 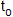 ) )
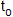 > 2.31 ( à 8 ddl)
(test bilatéral, il y autant de chance d’observer des écarts positifs que des écarts négatifs) > 2.31 ( à 8 ddl)
(test bilatéral, il y autant de chance d’observer des écarts positifs que des écarts négatifs)
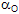 < 5% (et même < 5% (et même 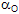 < 0.1% !!!) < 0.1% !!!)
Ho est rejetée, au seuil de 0.1%,
les différences sont significatives au seuil de 1 pour mille.
Au seuil de 0.1% on peut dire que la production est machine dépendante.
Comparaison de 2 moyennes sur séries appariées
Cas où n est supérieur à 30
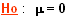
 population d’origine commune / différences dues au hasard population d’origine commune / différences dues au hasard
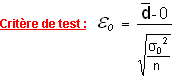
On se sert de la table échantillonnée de la loi normale centrée réduite pour trouver les valeurs de la probabilité 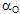 connaissant connaissant 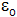 ou celles de ou celles de 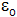 connaissant connaissant 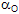 . .
On utilise la variance expérimentale des différences, n est le nombre de paires
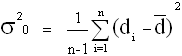
Permet de contrôler le paramètre toutes choses égales par ailleurs
 évite les effets de variances inter échantillon (puisqu’on travaille avec le même échantillon) évite les effets de variances inter échantillon (puisqu’on travaille avec le même échantillon)
Comparaison de 2 moyennes sur séries appariées
Petits échantillons n inférieur à 30
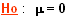
 population d’origine commune / différences dues au hasard population d’origine commune / différences dues au hasard
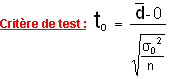
On se sert de la table échantillonnée de la loi de student pour trouver les valeurs de la probabilité 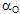 connaissant to ou celles de to connaissant connaissant to ou celles de to connaissant 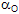 .
Attention : le nombre de degrés de liberté est ici : .
Attention : le nombre de degrés de liberté est ici : 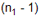 ddl ddl
Validité : la variable d doit être normale dans la population d’origine
Permet de contrôler le paramètre toutes choses égales par ailleurs
 évite les effets de variances inter échantillon (puisqu’on travaille avec le même échantillon) évite les effets de variances inter échantillon (puisqu’on travaille avec le même échantillon)
Comparaison de 2 moyennes sur séries appariées
N° de l'animal |
Taux de l'enzyme avant traitement [mg/ml] |
Taux de l'enzyme au cours du traitement [mg/ml] |
différences 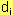 |
1 |
2,75 |
2,36 |
-0,39 |
2 |
3,14 |
2,88 |
-0,26 |
3 |
3,01 |
2,62 |
-0,39 |
4 |
3,4 |
3,14 |
-0,26 |
5 |
3,53 |
3,01 |
-0,52 |
6 |
3,14 |
2,75 |
-0,39 |
7 |
3,01 |
2,75 |
-0,26 |
8 |
3,66 |
3,01 |
-0,65 |
9 |
3,27 |
2,88 |
-0,39 |
10 |
2,88 |
2,62 |
-0,26 |
11 |
3,92 |
3,27 |
-0,65 |
12 |
3,66 |
3,14 |
-0,52 |
13 |
2,75 |
2,36 |
-0,39 |
14 |
3,14 |
2,88 |
-0,26 |
15 |
3,01 |
2,62 |
-0,39 |
|
| |
| |
Moyenne écart-type |
-0,40 |
| |
|
0,13 |
|
| Test d'homogénéité : |
|
|
| |
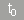 |
11,50 |
| |
 |
5,0 % |
| Ho rejetée au seuil 5% |
 |
0,0 % |
| |
 |
14 |
|
|
6. Tests du Khi-deux (non paramétrique)
Loi du Chi-deux 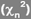 à n degrés de liberté (ddl) à n degrés de liberté (ddl)
Si 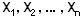 sont n variables indépendantes, suivant toutes une loi normale sont n variables indépendantes, suivant toutes une loi normale 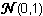
La variable 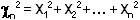 suit la suit la 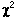 à n degrés de liberté (ddl). à n degrés de liberté (ddl).
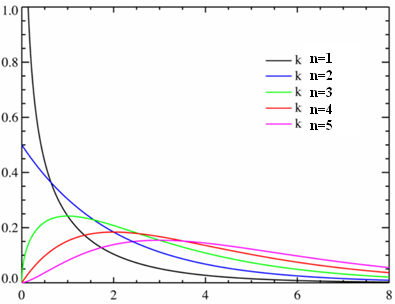
L'expression de la densité de probabilité est un peu compliquée
Pour n>2, maximum à (n-2)
Si n > 30, la loi tend vers une N (n,(2n)½ )
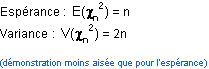
L'intervalle de confiance d'une variance
Emprunte à la loi 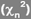 à n degrés de liberté (ddl) à n degrés de liberté (ddl)

Test de conformité / ajustement - Tableau de contingences
Ho : loi de distribution des classes connue ou supposée connue
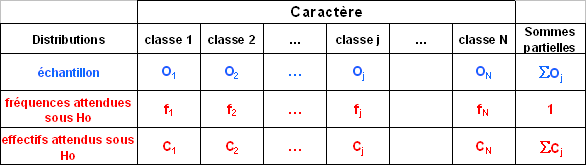
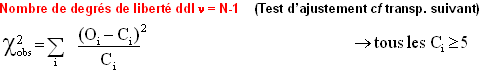

Exemple : Test de conformité
On compare un échantillon à une population pour laquelle la répartition pour la couleur des yeux est connue.
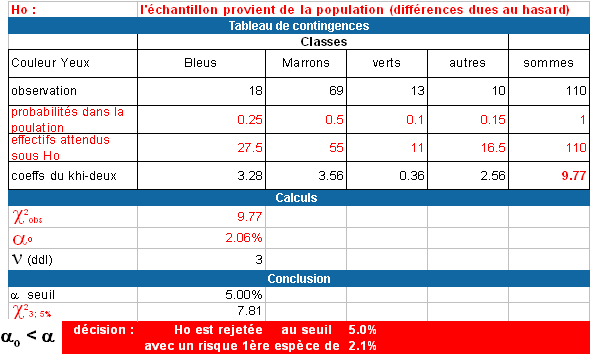

Exemple : Chi-deux d'ajustement à une loi de distribution (uniforme)
- On cherche à savoir si le dé utilisé est pipé
- On dispose des résultats de 90 lancés du dé

Tests d’ajustements - détermination du nombre de ddl
Ho : loi de distribution à  paramètres dont k sont déduits de l'échantillon. paramètres dont k sont déduits de l'échantillon.

Test d'homogénéité - Tableau de contingences
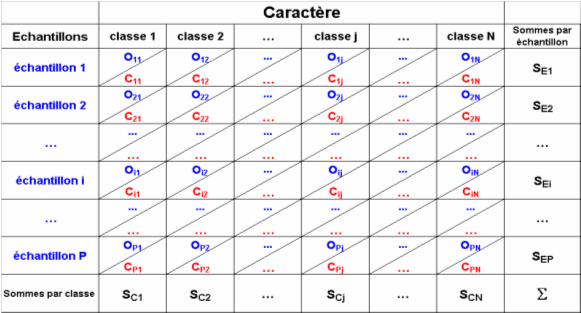
Ho : homogénéité des échantillons
=> il existe une population commune d'où sont issus tous les échantillons
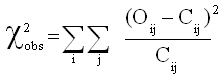
Ho : loi de distribution des classes connue ou supposée connue

Ho : Homogénéité des échantillons
=> Il existe une population d’origine commune d’où sont issus tous les échantillons
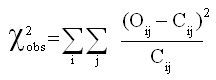

Exemple : Test d'homogénéité
Ho : les 2 échantillons sont homogènes pour l'expression des gènes dans les 9 catégories
=> Il existe une population commune (d’où sont issus les 2 échantillons)
 Nous allons construire un tableau de contingence sous Excel pour effectuer ce test Nous allons construire un tableau de contingence sous Excel pour effectuer ce test
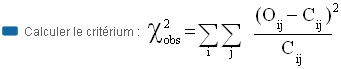
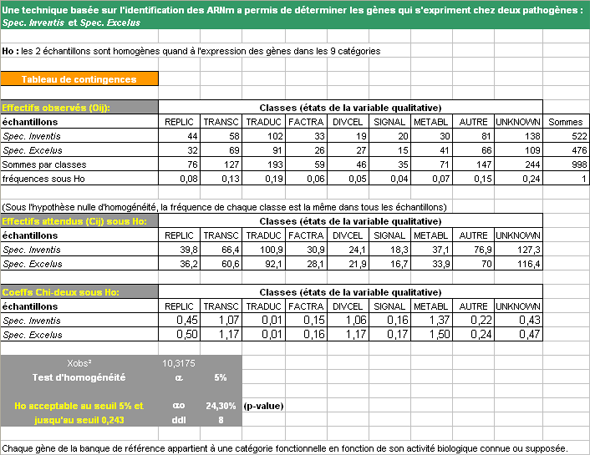
 Nous allons effectuer ce test sous Excel et ensuite ... R Nous allons effectuer ce test sous Excel et ensuite ... R
Test d'indépendance : un cas particulier du test d'homogénéité
Ho : Les 2 caractères sont indépendants
(les K échantillons portant les données sont homogènes)
H1 : Il existe une liaison entre les deux caractères
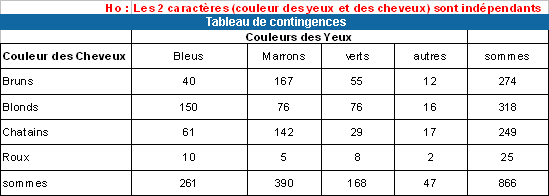
 Nous allons effectuer ce test sous Excel et ensuite ... R Nous allons effectuer ce test sous Excel et ensuite ... R
Exemple : Chi-deux d'ajustement
- On cherche à savoir si l’incidence d’une maladie a un caractère saisonnier. On dispose des dates de diagnostic de 120 cas :


|